
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng đường thẳng MN song song với giao tuyến d của hai mặt phẳng (SBC) và (SAD).

Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b song song với a

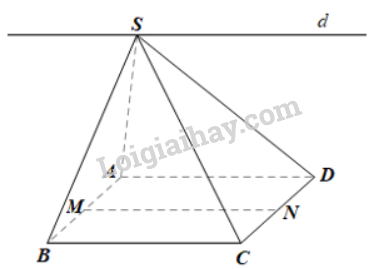
Ta có: S ∈ (SAD) và S ∈ (SBC) nên S là giao điểm của (SAD) và (SBC).
Lại có: AD // BC (do ABCD là hình bình hành);
AD ⊂ (SAD);
BC ⊂ (SBC).
Advertisements (Quảng cáo)
Do đó giao tuyến d của hai mặt phẳng (SAD) và (SBC) là đường thẳng đi qua S và song song với AD, BC.
Vì M, N lần lượt là trung điểm của AB và CD nên MN là đường trung bình
Do đó MN // BC // AD.
Ta có: MN // BC mà BC ⊂ (SBC) nên MN // (SBC);
MN // AD mà AD ⊂ (SAD) nên MN // (SAD).
Có: MN // (SBC);
MN // (SAD);
(SAD) ∩ (SBC) = d
Suy ra MN // d.
