
Cho hình tứ diện ABCD. Gọi I là trung điểm cạnh CD. Gọi M, N lần lượt là trọng tâm các tam giác BCD, CDA.
a) Chứng minh rằng các điểm M, N thuộc mặt phẳng (ABI)
b) Gọi G là giao điểm của AM và BN. Chứng minh rằng: \(\frac{{GM}}{{GA}} = \frac{{GN}}{{GB}} = \frac{1}{3}\)
c) Gọi P, Q lần lượt là trọng tâm các tam giác DAB, ABC. Chứng minh rằng các đường thẳng CP, DQ cùng đi qua điểm G và \(\frac{{GP}}{{GC}} = \frac{{GQ}}{{GD}} = \frac{1}{3}\)

- Muốn tìm giao điểm của một đường thẳng a và mặt phẳng (P), ta tìm giao điểm của a và một đường thẳng b nằm trong (P):
\(\left\{ \begin{array}{l}a \cap b = M\\b \subset (P)\end{array} \right. \Rightarrow M = a \cap (P)\)
Bước 1: Xác định mp (Q) chứa a
Bước 2: Tìm giao tuyến \(b = (P) \cap (Q)\)
Bước 3: Trong \((Q):a \cap b = M\) mà \(b \subset (P)\)suy ra \(M = a \cap (P)\)

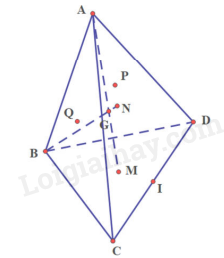
a) Ta có: M là trọng tâm của tam giác BCD
Nên M nằm trên trung tuyến BI (1)
Ta có: N là trọng tâm của tam giác ACD
Nên N nằm trên trung tuyến AI (2)
Từ (1) và (2) suy ra M và N thuộc mp (ABI)
b) Gọi H, K lần lượt là trung điểm của AG, BG
Advertisements (Quảng cáo)
Ta có: HK // AB
AB // MN
Suy ra MN // HK
Theo định lý Ta-let, ta có: \(\frac{{GM}}{{GH}} = \frac{{GN}}{{GK}} = \frac{{MN}}{{HK}}(1)\)
Ta có:\(\frac{{HK}}{{AB}} = \frac{1}{2},\frac{{MN}}{{AB}} = \frac{1}{3}\)
Do đó \(\frac{{MN}}{{AB}}:\frac{{HK}}{{AB}} = \frac{2}{3} \Rightarrow \frac{{MN}}{{HK}} = \frac{2}{3}(2)\)
Từ (1) và (2) suy ra\(\frac{{GM}}{{GH}} = \frac{2}{3}GH = \frac{1}{2}GA \Rightarrow \frac{{GM}}{{\frac{1}{2}GA}} = \frac{2}{3} \Rightarrow \frac{{GM}}{{GA}} = \frac{1}{3}\)
Chứng minh tương tự ta được\(\frac{{GN}}{{GB}} = \frac{1}{3}\)
c) Gọi H, K lần lượt là trung điểm của BC, BD
Tam giác AHD có:\(\frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)
Suy ra: QM // AD
Do đó, tam giác QGM đồng dạng với tam giác DGA
Nên D, G, Q thẳng hàng
Ta có: QM // AD nên \(\frac{{QM}}{{AD}} = \frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)
Mà \(\frac{{QM}}{{AD}} = \frac{{QG}}{{GD}}\)
Do đó:\(\frac{{QG}}{{GD}} = \frac{1}{3}\)
Chứng minh tương tự ta được\(\frac{{GP}}{{GC}} = \frac{1}{3}\)
Suy ra điều cần chứng minh.
