I. Giới hạn hữu hạn của hàm số tại một điểm
1. Định nghĩa
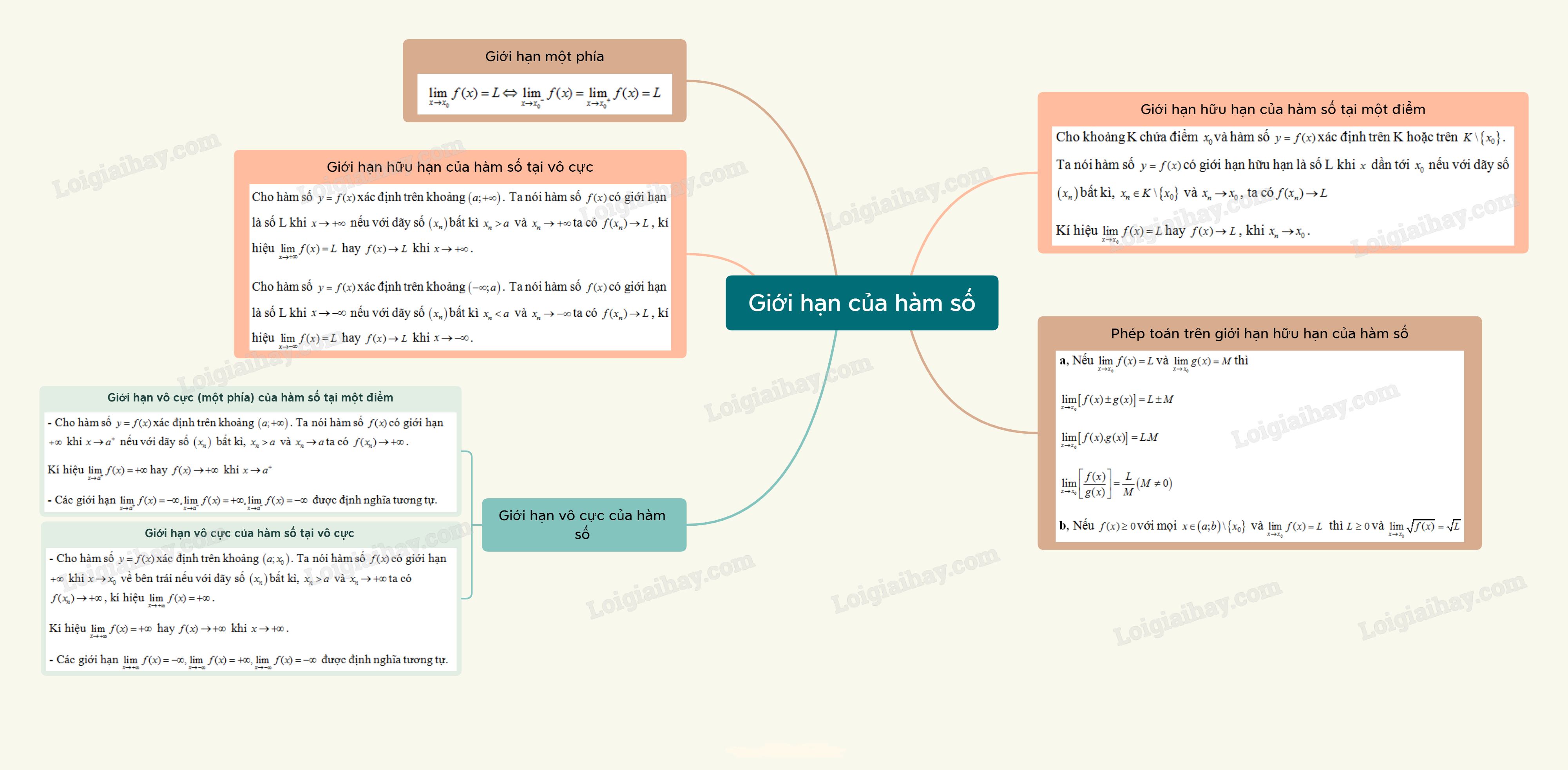
Cho khoảng K chứa điểm \({x_0}\)và hàm số \(f(x)\) xác định trên K hoặc trên \(K\backslash \left\{ {{x_0}} \right\}\). Hàm số \(f(x)\)có giới hạn là số L khi \(x\) dần tới \({x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\)bất kì, \({x_n} \in K\backslash \left\{ {{x_0}} \right\}\) và \({x_n} \to {x_0}\), ta có\(f({x_n}) \to L\)
Kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) hay \(f(x) \to L\), khi \({x_n} \to {x_0}\).
2. Phép toán trên giới hạn hữu hạn của hàm số
a, Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) và \(\mathop {\lim }\limits_{x \to {x_0}} g(x) = M\)\(\left( {L,M \in \mathbb{R}} \right)\)thì
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x) \pm g(x)} \right] = L \pm M\)
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x).g(x)} \right] = L.M\)
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {\frac{{f(x)}}{{g(x)}}} \right] = \frac{L}{M}\left( {M \ne 0} \right)\)
b, Nếu \(f(x) \ge 0\) với mọi \(x \in \left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}\) và \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) thì \(L \ge 0\) và \(\mathop {\lim }\limits_{x \to {x_0}} \sqrt {f(x)} = \sqrt L \).
3. Giới hạn một phía
- Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a;{x_0}} \right)\). Số L được gọi là giới hạn bên trái của hàm số \(y = f(x)\) khi \(x \to {x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì thỏa mãn \(a < {x_n} < {x_0}\) và \({x_n} \to {x_0}\) ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = L\).
- Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {{x_0};b} \right)\). Số L là giới hạn bên của hàm số \(y = f(x)\) khi \(x \to {x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\)bất kì thỏa mãn \({x_0} < {x_n} < b\) và \({x_n} \to {x_0}\) ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L\).
*Nhận xét: \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = \mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L\)
II. Giới hạn hữu hạn của hàm số tại vô cực
Advertisements (Quảng cáo)
- Cho hàm số \(y = f(x)\)xác định trên khoảng \(\left( {a; + \infty } \right)\). Ta nói hàm số \(f(x)\) có giới hạn là số L khi \(x \to + \infty \) nếu với dãy số \(\left( {{x_n}} \right)\)bất kì \({x_n} > a\) và \({x_n} \to + \infty \)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = L\) hay \(f(x) \to L\) khi \(x \to + \infty \).
- Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( { - \infty ;b} \right)\). Ta nói hàm số \(f(x)\) có giới hạn là số L khi \(x \to - \infty \) nếu với dãy số \(\left( {{x_n}} \right)\)bất kì \({x_n} < b\) và \({x_n} \to - \infty \)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = L\) hay \(f(x) \to L\) khi \(x \to - \infty \).
* Nhận xét:
- Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.
- Với c là hằng số, k là một số nguyên dương ta có:
\(\mathop {\lim }\limits_{x \to + \infty } c = c\), \(\mathop {\lim }\limits_{x \to - \infty } c = c\),\(\mathop {\lim }\limits_{x \to + \infty } (\frac{c}{{{x^k}}}) = 0,\mathop {\lim }\limits_{x \to - \infty } (\frac{c}{{{x^k}}}) = 0\).
III. Giới hạn vô cực (một phía) của hàm số tại một điểm
- Cho hàm số \(y = f(x)\)xác định trên khoảng \(\left( {a; + \infty } \right)\). Ta nói hàm số \(f(x)\)có giới hạn \( + \infty \) khi \(x \to {a^ + }\) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} > a\) và \({x_n} \to a\)ta có \(f({x_n}) \to + \infty \).
Kí hiệu \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = + \infty \)hay \(f(x) \to + \infty \) khi \(x \to {a^ + }\)
- Các giới hạn \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = - \infty ,\mathop {\lim }\limits_{x \to {a^ - }} f(x) = + \infty ,\mathop {\lim }\limits_{x \to {a^ - }} f(x) = - \infty \) được định nghĩa tương tự.
IV. Giới hạn vô cực của hàm số tại vô cực
- Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a;{x_0}} \right)\). Ta nói hàm số \(f(x)\)có giới hạn \( + \infty \) khi \(x \to {x_0}\) về bên trái nếu với dãy số \(\left( {{x_n}} \right)\)bất kì, \({x_n} > a\) và \({x_n} \to + \infty \) ta có \(f({x_n}) \to + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \).
Kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \) hay \(f(x) \to + \infty \) khi \(x \to + \infty \).
- Các giới hạn \(\mathop {\lim }\limits_{x \to + \infty } f(x) = - \infty ,\mathop {\lim }\limits_{x \to - \infty } f(x) = + \infty ,\mathop {\lim }\limits_{x \to - \infty } f(x) = - \infty \) được định nghĩa tương tự.
* Chú ý:
- \(\mathop {\lim }\limits_{x \to + \infty } {x^k} = + \infty ,k \in {\mathbb{Z}^ + }.\)
- \(\mathop {\lim }\limits_{x \to - \infty } {x^k} = + \infty ,\) k là số nguyên dương chẵn.
- \(\mathop {\lim }\limits_{x \to - \infty } {x^k} = - \infty ,\) k là số nguyên dương lẻ.