
Vũ và Tâm đều theo dõi thành tích của các vận động viên nam trong một cuộc thi bơi tự do dài 50 m. Vũ ghi lại thời gian bơi (đơn vị: giây) của mỗi vận động viên, còn Tâm lập bảng phân bố tần số ghép lớp để biểu diễn kết quả.
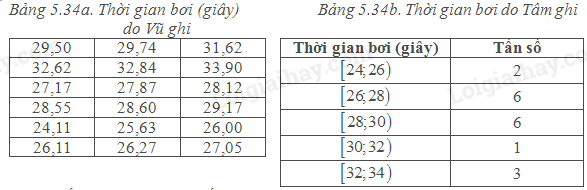
a) Với số liệu do Vũ cung cấp, hãy tính thành tích trung bình của các vận động viên.
b) Với bảng tấn số ghép nhóm của Tâm thì thành tích trung bình của các vận động viên là bao nhiêu?
c) Giải thích vì sao có sự khác nhau giữa hai kết quả tìm được.

a) Số liệu do Vũ ghi theo dạng liệt kê nên trung bình tính theo công thức \(\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}\)
b) \(\overline x \) của mẫu số liệu ghép nhóm được tính theo công thức
\(\overline x = \frac{1}{N}\left( {{c_1}{n_1} + {c_2}{n_2} + ... + {c_k}{n_k}} \right)\) với \({c_k},{n_k}\) lần lượt là giá trị đại diện và tần số của nhóm thứ k
Advertisements (Quảng cáo)
\({c_k}\) là trung bình cộng của đầu mút trái và đầu mút phải của nhóm đó.
c) Dựa vào ý nghĩa của công thức tính số trung bình với bảng tần số ghép nhóm

a) Thành tích trung bình của các vận động viên là
\(\overline x = \frac{{29,50 + 29,74 + ... + 27,05}}{{18}} = 28,01\) giây
b) Để ngắn gọn, ta trình bày cách tính trung bình của mẫu số liệu ghép nhóm qua bảng sau
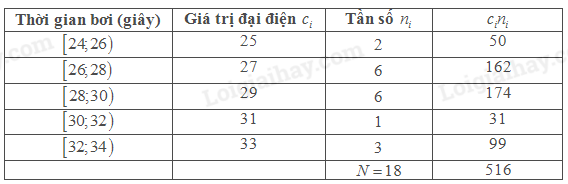
Số trung bình của mẫu số liệu là \(\overline x = \frac{{516}}{{18}} \approx 28,67\) giây
c) Do đối với một mẫu số liệu ghép nhóm, do không biết từng số liệu cụ thể nên ra không tính được giá trị chính xác của số trung bình mà chỉ có thể ước tính gần đúng số trung bình của mẫu.
