
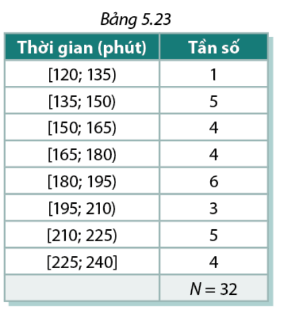
Bảng 5.23 biểu diễn kết quả thống kê về thời gian cần thiết để thực hiện cuộc chạy marathon đã được tổ chức ở một địa phương .
a, Xác định các tứ phân vị của mẫu số liệu
b, Xét nhóm gồm 50 % số cuộc thi có thời gian ngắn hơn đã được tổ chức. Thời gian tối đa của các cuộc thi trong nhóm này là bao nhiêu?


a, Sử dụng công thức tính các tứ phân vị
b, Thời gian tối đa của các cuộc thi trong nhóm này là \({Q_1}\)

Advertisements (Quảng cáo)
a, Bảng tần số tích lũy mẫu số liệu
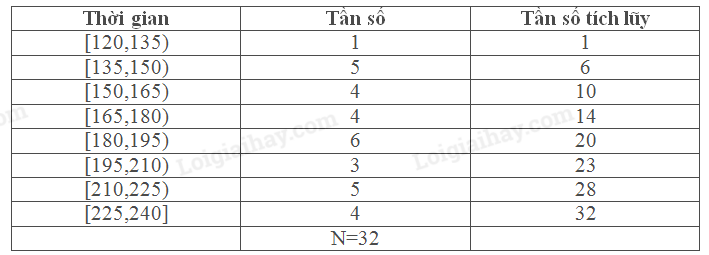
Ta có: \(\frac{N}{4} = \frac{{32}}{4} = 8 \Rightarrow \frac{N}{2} = 16 \Rightarrow \frac{{3N}}{4} = 24\)
Các nhóm chứa \({Q_1}\), \({Q_2}\) và \({Q_3}\) là [150,165), [180,195) và [210,225)
Độ dài các nhóm ghép đều là h=15
Ta có: \({L_1} = 150,{n_1} = 4,{T_1} = 6\)\( \Rightarrow {Q_1} = {L_1} + \frac{{\frac{N}{4} - {T_1}}}{{{n_1}}}.h = 150 + \frac{{8 - 6}}{4}.15 = 157,5\)
\({L_2} = 180,{n_2} = 6,{T_2} = 14\)\( \Rightarrow {Q_2} = {L_2} + \frac{{\frac{N}{2} - {T_2}}}{{{n_2}}}.h = 180 + \frac{{16 - 14}}{6}.15 = 185\)
\({L_3} = 210,{n_3} = 5,{T_3} = 23\)\( \Rightarrow {Q_3} = {L_3} + \frac{{\frac{{3N}}{4} - {T_3}}}{{{n_3}}}.h = 210 + \frac{{24 - 23}}{5}.15 = 213\)
b, Thời gian tối đa của các cuộc thi trong nhóm này là \({Q_1}\)=157,5 phút .
