
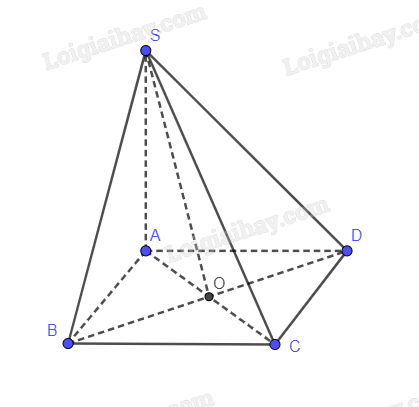
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, \(SA \bot \left( {ABCD} \right)\). Biết số đo của góc nhị diện \(\left[ {S,BD,A} \right]\) bằng 450, tính chiều cao của hình chóp.

Cách tìm số đo của góc nhị diện \(\left[ {S,CD,A} \right]\):
+ Tìm giao tuyến d của (SCD) và (ACD).
+ Tìm \(a \subset \left( {SCD} \right)\) vuông góc với d. Tìm \(b \subset \left( {ACD} \right)\) vuông góc với d.
+ Tính \(\left( {a,b} \right)\).

Advertisements (Quảng cáo)
SA vuông góc với BD (Vì SA vuông góc với (ABCD))
AC vuông với BD (Vì ABCD là hình vuông)
Nên (SAC) vuông với BD
Trong (ABCD), gọi O là giao điểm của AC và BD
Suy ra SO vuông góc với BD
Mà: AO vuông góc với BD
Suy ra góc phẳng nhị diện \(\left[ {S,BD,A} \right]\) là góc SOA
Hình vuông ABCD có cạnh 2a nên AC = \(2\sqrt 2 a\). Suy ra AO = \(\sqrt 2 a\)
\(\tan \widehat {SOA} = \,\frac{{SA}}{{AO}} \Leftrightarrow \tan {45^0} = \frac{{SA}}{{\sqrt 2 a}} \Leftrightarrow SA = \sqrt 2 a\)
