
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a và điểm A’ cách đều các điểm A, B, C. Biết AA’ = 2a, tính thể tích khối lăng trụ này.

Công thức tính thể tích hình lăng trụ: V = S.h với S là diện tích đáy, h là chiều cao.

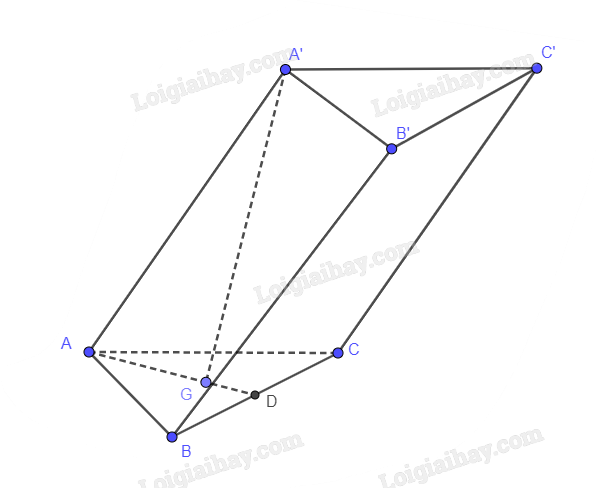
Gọi D là trung điểm của AC, G là trọng tâm tam giác ABC
Advertisements (Quảng cáo)
A’.ABC là chóp tam giác đều nên A’G vuông góc với (ABC). Suy ra A’G là chiều cao của hình lăng trụ
Tam giác ABC đều có cạnh bằng a nên BD vuông góc với AC
Ta có: \(BD = \sqrt {A{B^2} - A{D^2}} = \sqrt {{a^2} - {{\left( {\frac{1}{2}a} \right)}^2}} = \frac{{\sqrt 3 }}{2}a\)
\(BG = \frac{2}{3}BD = \frac{{\sqrt 3 }}{3}a\)
Xét tam giác vuông A’BG vuông tại G có:
\(A’G = \sqrt {A'{B^2} - B{G^2}} = \sqrt {{{\left( {2a} \right)}^2} - {{\left( {\frac{{\sqrt 3 }}{3}a} \right)}^2}} = \frac{{\sqrt {33} }}{3}a\)
\(V = S.h = \frac{1}{2}.BD.AC.A’G = \frac{1}{2}.\frac{{\sqrt 3 }}{2}a.a.\frac{{\sqrt {33} }}{3}a = \frac{{\sqrt {11} }}{4}{a^3}\)
