
Cho tứ diện ABCD có hai mặt ABC và DBC là hai tam giác cân chung đáy BC. Trong các mệnh đề sau, mệnh đề nào đúng?
A. AB \( \bot \) CD.
B. AC \( \bot \) BD.
C. AD \( \bot \) BC.
D. AB \( \bot \) AD.

Để chứng minh a vuông góc b ta đi chứng minh a vuông góc với (P) chứa b.

Advertisements (Quảng cáo)
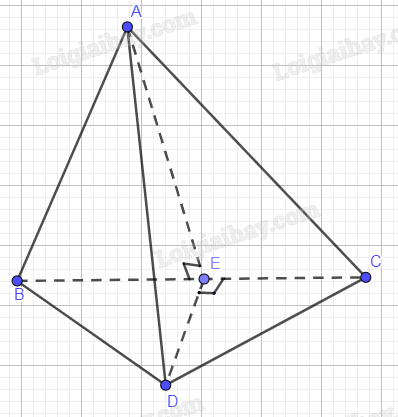
Tam giác ABC cân tại A nên AE là đường cao đồng thời là đường trung tuyến \( \Rightarrow \) E là trung điểm BD \( \Rightarrow \)CE là đường trung tuyến của tam giác BCD.
Mà tam giác BDC cân tại D nên CE là đường cao hay \(CE \bot BD\).
Ta có:
\(\left\{ \begin{array}{l}AE \bot BC\\DE \bot BC\\AE \cap DE = E\\AE,DE \subset (ADE)\end{array} \right. \Rightarrow BC \bot (ADE)\)
Do đó,
\(\left\{ \begin{array}{l}BC \bot (ACE)\\AD \subset (ADE)\end{array} \right. \Rightarrow BC \bot AD\)
Chọn đáp án C.
