Trả lời - Bài 8.8 trang 63 SGK Toán 11 tập 2 - Cùng khám phá - Bài 2 - Đường thẳng vuông góc với mặt phẳng. Phép chiếu vuông góc. Cho tứ diện ABCD biết ABC và BCD là hai tam giác cân có chung cạnh đáy BC . Gọi I là trung điểm cạnh BC. Chứng minh \(BC \bot (ADI)\)...

Cho tứ diện ABCD biết ABC và BCD là hai tam giác cân có chung cạnh đáy BC . Gọi I là trung điểm cạnh BC. Chứng minh \(BC \bot (ADI)\).

Dựa vào tam giác cân để suy ra \(AI \bot BC\) và \(DI \bot BC\)

Advertisements (Quảng cáo)
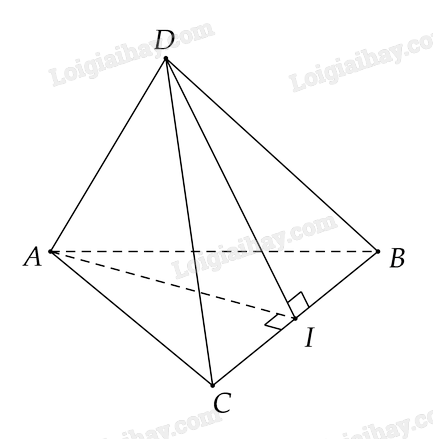
Vì \(\Delta ABC\) cân tại \(A\) và \(I\) là trung điểm của \(BC\) nên \(AI \bot BC\)
Vì \(\Delta DBC\) cân tại \(D\) và \(I\) là trung điểm của \(BC\) nên \(DI \bot BC\)
Ta có \(\left\{ \begin{array}{l}BC \bot AI\\BC \bot DI\end{array} \right. \Rightarrow BC \bot \left( {AID} \right)\)
