I. Nhóm chứa trung vị
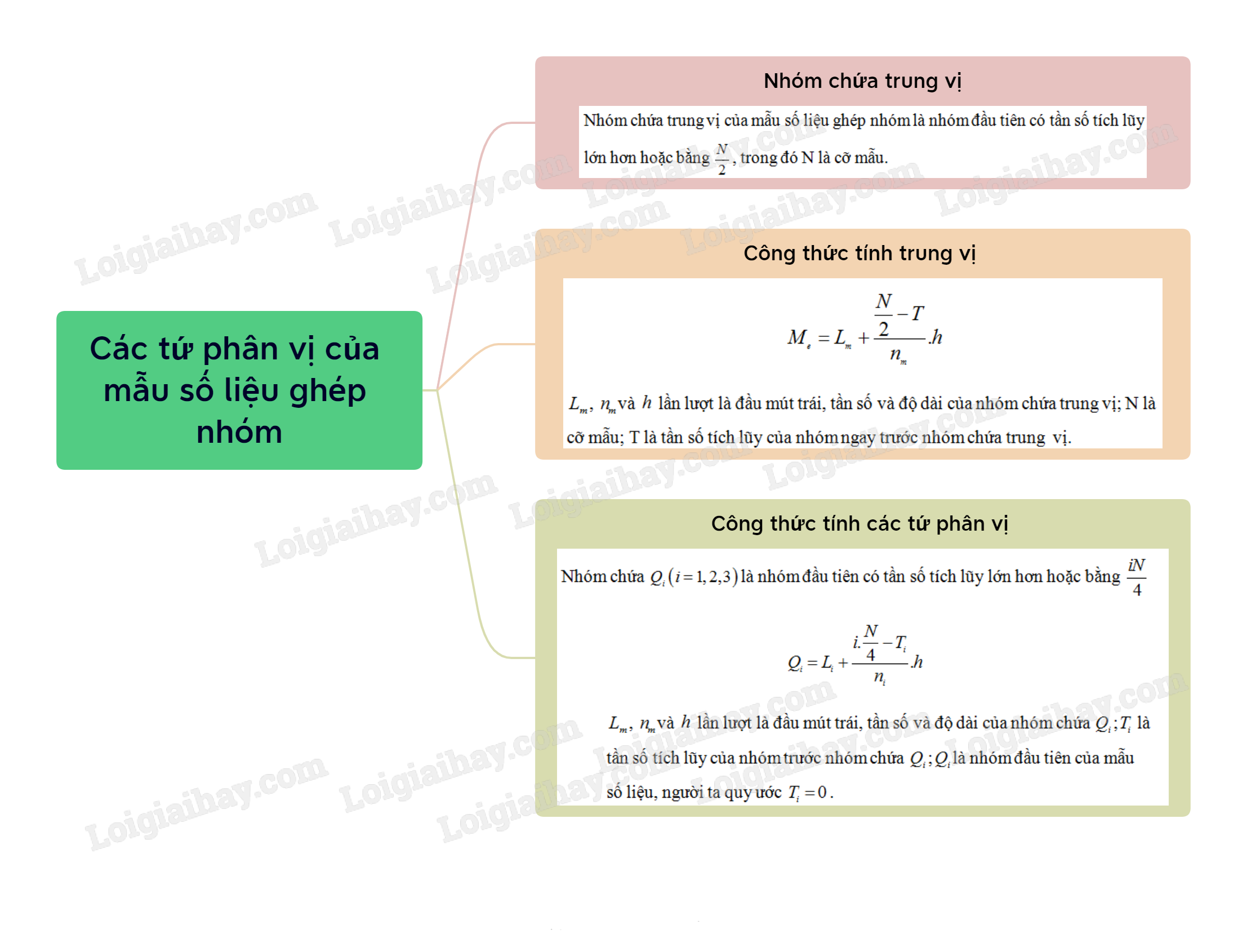
Nhóm chứa trung vị của mẫu số liệu ghép nhóm là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{N}{2}\), trong đó N là cỡ mẫu.
II. công thức tính trung vị của mẫu số liệu ghép nhóm
\({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h\)
Trong đó:
- N là cỡ mẫu
- \({L_m}\), \({n_m}\) và \(h\) lần lượt là đầu mút trái, tần số và độ dài của nhóm chứa trung vị.
- T là tần số tích lũy của nhóm ngay trước nhóm chứa trung vị.
- Trong trường hợp nhóm chứa trung vị là nhóm đầu tiên của mẫu số liệu, người ta quy ước \(T = 0\).
* Ý nghĩa: Trung vị của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho trung vị của mẫu số liệu và có thể sử dụng làm giá trị đại diện cho mẫu số liệu.
III. Công thức tính các tứ phân vị của mẫu số liệu ghép nhóm
Công thức tính các tứ phân vị \({Q_1},{Q_2},{Q_3}\) của mẫu số liệu ghép nhóm:
Advertisements (Quảng cáo)
Nhóm chứa \({Q_i}\left( {i = 1,2,3} \right)\) là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{{iN}}{4}\) và
\({Q_i} = {L_i} + \frac{{i.\frac{N}{4} - {T_i}}}{{{n_i}}}.h\)
Trong đó:
- N là cỡ mẫu .
- \({L_i}\), \({n_i}\) và \(h\) lần lượt là đầu mút trái, tần số và độ dài của nhóm chứa \({Q_i}\).
- \({T_i}\) là tần số tích lũy của nhóm trước nhóm chứa \({Q_i}\).
- \({Q_i}\) là nhóm đầu tiên của mẫu số liệu, người ta quy ước \({T_i} = 0\).
* Lưu ý: Trong trường hợp các nhóm có độ dài bằng nhau thì h giống nhau với mọi nhóm.
* Ý nghĩa:
- Tứ phân vị của mẫu số liệu ghép nhóm là giá trị xấp xỉ của tứ phân vị của mẫu số liệu.
- Các tứ phân vị \({Q_1},{Q_2},{Q_3}\) chia mẫu số liệu ghép nhóm thành 4 phần có số liệu bằng nhau. Các tứ phân vị cho ta một hình ảnh về sự phân bố của mẫu số liệu. Dựa vào các tứ phân vị, ta có thể biết số liệu tập trung ít hay nhiều quanh trung vị.