Hoạt động 1
Viết công thức tính thể tích khối lăng trụ đứng tam giác (Hình 8.68) và khối lăng trụ đứng tứ giác (Hình 8.69) theo diện tích đáy S và đường cao h của nó.
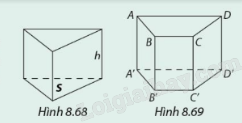

V = S.h

Công thức tính thể tích khối lăng trụ đứng: V = S.h
Luyện tập 1
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a , góc giữa cạnh bên và mặt đáy bằng 300. Hình chiếu của A’ trên (ABC) là trung điểm I của cạnh BC. Tính thể tích khối lăng trụ này.

Công thức tính thể tích khối lăng trụ: V = S.h
Advertisements (Quảng cáo)
S: diện tích đáy, h: chiều cao

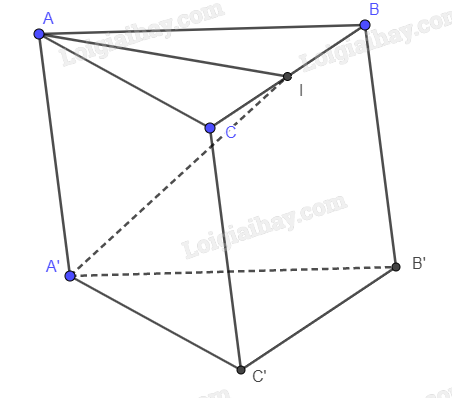
Gọi I là trung điểm BC
\(AI = \sqrt {A{C^2} - I{C^2}} = \sqrt {{a^2} - {{\left( {\frac{1}{2}a} \right)}^2}} = \frac{{\sqrt 3 }}{2}a\)
Tam giác AB đều nên AI vuông góc với BC hay AI vuông góc với (ABC)
Suy ra \(\widehat {\left( {AA’,\left( {ABC} \right)} \right)} = \widehat {A’AI} = {30^0}\)
I là hình chiếu của A’ trên (ABC) nên A’I vuông góc với BC
Suy ra tam giác A’AI vuông tại I có:
\(\tan {30^0} = \frac{{A’I}}{{AI}} = \frac{{A’I}}{{\frac{{\sqrt 3 }}{2}a}} \Rightarrow A’I = \frac{1}{2}a\)
\(V = {S_{\Delta ABC}}.A’I = \frac{1}{2}AI.BC.A’I = \frac{1}{2}.\frac{{\sqrt 3 }}{2}a.a.\frac{1}{2}a = \frac{{\sqrt 3 }}{8}{a^3}\)
