Hoạt động 6
Cho hình hộp chữ nhật ABCD.A’B’C’D’. Xét hai đường thẳng chéo nhau AA’ và DC’
a) Đường thẳng A’D’ có đồng thời cắt và vuông góc với hai đường thẳng AA’ và D’C không? Vì sao?
b) Tìm mặt phẳng \(\left( \alpha \right)\) chứa đường thẳng AA’ và song song với D’C. So sánh d(D’C, \(\left( \alpha \right)\)) và A’D’.
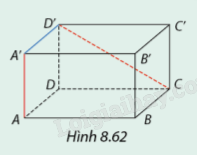

Quan sát hình vẽ.

a) Đường thẳng A’D’ không đồng thời cắt và vuông góc với hai đường thẳng AA’ và D’C vì A’D’ không vuông góc với D’C.
b) \(\left( \alpha \right)\) là (AA’B)
d(D’C, (AA’B)) = A’D’.
Luyện tập 6
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), SA = 3a; ABCD là hình vuông cạnh a, O là giao điểm của AC và BD. Tính khoảng cách giữa:
a) BD và SC
b) AB và SC.

a) Tìm khoảng cách giữa a và b:
Advertisements (Quảng cáo)
+ Tìm (P) chứa a và vuông góc với b.
+ Tìm giao điểm H thỏa mãn thuộc b và nằm trong (P).
+ Tại (P), dựng HK vuông góc với a tại K.
+ HK là khoảng cách cần tìm.
b) Tìm khoảng cách giữa a và b:
+ Tìm (P) chứa a và song song với b.
+ \(d\left( {a,b} \right) = d\left( {b,\left( P \right)} \right)\).

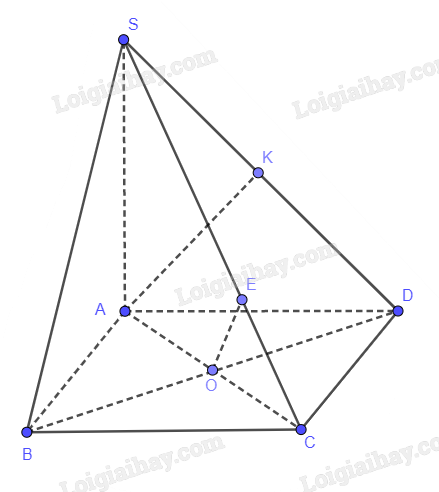
a) BD vuông góc với (SAC)
Kẻ OE vuông góc với SC
Vậy OE là khoảng cách cần tìm
\(\begin{array}{l}\frac{1}{{O{E^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{9{a^2}}} + \frac{1}{{2{a^2}}}\\ \Rightarrow OE = \frac{{3\sqrt {22} }}{{11}}a\end{array}\)
b) Kẻ AK vuông góc với SD
Ta có: AB // CD nên AB // (SCD)
\(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCD} \right)} \right) = AK\)
\(\begin{array}{l}AK.SD = SA.AD\\ \Leftrightarrow AK = \frac{{3a.a}}{{\sqrt {{{\left( {3a} \right)}^2} + {a^2}} }} = \frac{{3\sqrt {10} }}{{10}}a\end{array}\)
