Bài 2. Chứng minh rằng nếu một hình nào đó có hai trục đối xứng vuông góc với nhau thì hình đó có tâm đối xứng

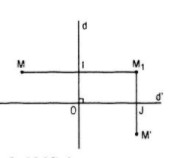
Giả sử hình H có hai trục đối xứng d và d’ vuông góc với nhau
Gọi O là giao điểm của hai trục đối xứng đó
Advertisements (Quảng cáo)
Lấy M là điểm bất kì thuộc hình H, M1 là điểm đối xứng với M qua d, M’ là điểm đối xứng với M1 qua d’
Vì d và d’ đều là trục đối xứng của hình H nên M1 và M’ đều thuộc H
Gọi I là trung điểm của MM1, J là trung điểm của M1M’ thì ta có:
\(\overrightarrow {OM} = \overrightarrow {OI} + \overrightarrow {IM} = \overrightarrow {M’J} + \overrightarrow {JO} = \overrightarrow {M’O} \) hay \(\overrightarrow {OM} + \overrightarrow {OM’} = \overrightarrow 0 \)
Vậy phép đối xứng tâm O biến điểm M thuộc hình H thành điểm M’ thuộc H, suy ra H có tâm đối xứng là O
