Cho hai đường tròn . Câu 30 trang 29 SGK Hình học 11 Nâng cao - Bài 6. Phép vị tự
Bài 30. Cho hai đường tròn (O) và (O’) có bán kính khác nhau, tiếp xúc ngoài với nhau tại A. Một đường tròn (o”) thay đổi, luôn luôn tiếp xúc ngoài với (O) và (O’) lần lượt tại B và C . Chứng minh rằng đường thẳng BC luôn đi qua một điểm cố định
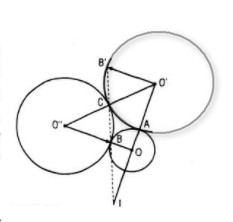
Kéo dài BC cắt (O’) tại B’
Advertisements (Quảng cáo)
Vì C là tâm vị tự trong của (O’) và (O”) nên hai vecto \(\overrightarrow {O’B} \) và \(\overrightarrow {O”B’} \) ngược hướng
Vì B là tâm vị tự trong của (O) và (O”) nên hai vecto \(\overrightarrow {O”B} \) và \(\overrightarrow {OB} \) ngược hướng
Vậy hai vecto \(\overrightarrow {OB} \) và \(\overrightarrow {O’B’} \) cùng hướng
Từ đó suy ra đường thẳng BB’, cũng chính là đường thẳng BC, luôn đi qua điểm cố định là tâm vị tự ngoài I của (O) và (O’)