Bài 11. Khoảng cách giữa hai cạnh đối của một tứ diện đều cạnh \(a\) là bằng:
(A) \({{3a} \over 2}\) (B) \({{a\sqrt 2 } \over 2}\)
(C) \({{a\sqrt 3 } \over 2}\) (D) \(a\sqrt2\)
Gọi \(I\) là trung điểm cạnh \(AB\)
\(J\) là trung điểm của cạnh \(CD\)
\(IJ\) là đoạn vuông góc của cạnh \(AB\) và \(CD\).
Độ dài của \(IJ\) là khoảng cách giữa hai cạnh đối \(AB\), (CD\) của tứ diện.
Advertisements (Quảng cáo)
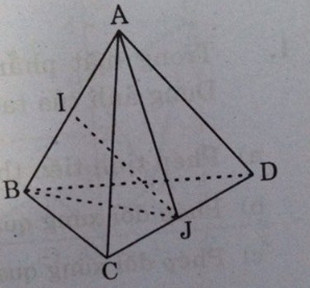
Tứ diện cạnh a nên:
\(\eqalign{
& BJ = {{a\sqrt 3 } \over 2},BI = {a \over 2} \cr
& \Rightarrow {\rm{I}}{{\rm{J}}^2} = B{J^2} - B{I^2} \cr
& \Rightarrow {\rm{I}}{{\rm{J}}^2} = {{2{a^2}} \over 4} \Rightarrow {\rm{I}}{{\rm{J}}^2} = {{a\sqrt 2 } \over 2} \cr} \)
