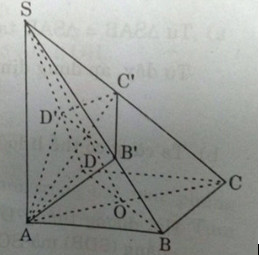
Bài 3. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh \(SA\) bằng \(a\) và vuông góc với mặt phẳng \((ABCD)\).
a) Chứng minh rằng bốn mặt bên của hình chóp là những tam giác vuông.
b) Mặt phẳng \((α)\) đi qua \(A\) và vuông góc với cạnh \(SC\) lần lượt cắt \(SB, SC\) và \(SD\) tại \(B’, C’\) và \(D’\). Chứng minh \(B’D’\) song song với \(BD\) và \(AB’\) vuông góc với \(SB\).
a)
\(SA ⊥(ABCD)\) nên \(AB\) là hình chiếu của \(SB\) trên \(mp(ABCD)\)
\(ABCD\) là hình vuông nên \(BC ⊥AB\). Ta có:
\(\left. \matrix{
SA \bot (ABCD) \hfill \cr
BC \bot AB \hfill \cr} \right\}\)
\(⇒ SB⊥BC\) (theo định lí ba đường vuông góc)
\(⇒ Δ SBC\) là tam giác vuông tại \( B\)
Chứng minh tương tự \(ΔSDA\) vuông tại \(D\)
\(SA ⊥(ABCD) ⇒ SA ⊥ AB ⇒ Δ SAB\) vuông tại \(A\)
\(SA\bot AD\)\( ⇒ Δ SAD\) vuông tại \(A\)
b)
\(\left. \matrix{
SA \bot DB \hfill \cr
AC \bot BD \hfill \cr} \right\} \Rightarrow DB \bot (SAC)\) (1)
Advertisements (Quảng cáo)
Ta lại có:
\(\eqalign{
& \left. \matrix{
BC \bot SB \hfill \cr
BC \bot AB \hfill \cr} \right\} \Rightarrow BC \bot (SAB);AB’ \subset (SAB)(2) \cr
& \Rightarrow AB’ \bot BC \cr
& \left. \matrix{
AB’ \subset (\alpha ) \hfill \cr
SC \bot (\alpha ) \hfill \cr} \right\} \Rightarrow AB’ \bot SC(3) \cr} \)
Chứng minh tương tự ta có: \(AD’⊥SC\)
Hai tam giác vuông \(SAB\) và \(SAD\) bằng nhau mà \(AB’\) và \(AD’\) là các đường cao tương ứng nên \(AD’= AB’\) (4)
Ta cũng có: \(SB’=SD’\);
\(ΔBSC = Δ DSC\) \(⇒ \widehat{ BSC} = \widehat{ CSD}\)
Do đó \(ΔB’SC’ = Δ D’SC’\)
Từ đây suy ra: \(C’D’ = C’B’\) (5)
Từ (4) và (5) suy ra \(A\) và \(C’\) nằm trên đường trung trực của \(D’B’\) do đó \(D’B’⊥ AC’\) (6)
Mặt khác: \(SC⊥(α)\); \(D’B’⊂ (α)\) \( ⇒ SC⊥D’B’\) (7)
Từ (6) và (7) suy ra: \(D’B’⊥(SAC)\) (8)
Từ (1) và (8) ta thấy rằng \(DB\) và \(D’B’\) cùng vuông góc với mặt phẳng \((SAC)\) nên \(D’B’//DB\)
Ta có:
\(\left. \matrix{
AB’ \bot BC \hfill \cr
AB’ \bot SC \hfill \cr} \right\} \Rightarrow AB’ \bot (SBC) \Rightarrow AB’ \bot SB\)
