
Chiều cao của một số cây giống sau khi nảy mầm được 4 tuần được biểu diễn ở bảng sau:
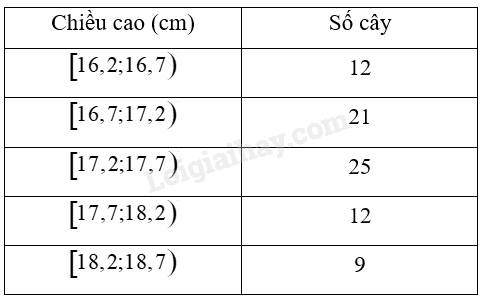
Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).

‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm:
\(\begin{array}{l}{S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}} \right]\\ & = \frac{1}{n}\left[ {{n_1}c_1^2 + {n_2}c_2^2 + ... + {n_k}c_k^2} \right] - {\overline x ^2}\end{array}\)
‒ Sử dụng công thức tính độ lệch chuẩn của mẫu số liệu ghép nhóm: \(S = \sqrt {{S^2}} \).

Advertisements (Quảng cáo)
Ta có bảng sau:
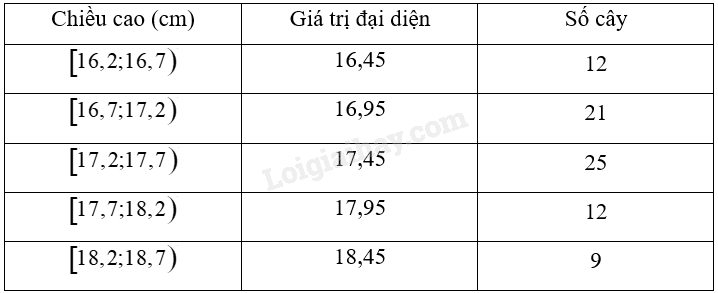
Cỡ mẫu \(n = 12 + 21 + 25 + 12 + 9 = 79\)
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline x = \frac{{12.16,45 + 21.16,95 + 25.17,45 + 12.17,95 + 9.18,45}}{{79}} \approx 17,3551\)
Phương sai của mẫu số liệu ghép nhóm đó là:
\({S^2} = \frac{1}{{79}}\left( {{{12.16,45}^2} + {{21.16,95}^2} + {{25.17,45}^2} + {{12.17,95}^2} + {{9.18,45}^2}} \right) - {17,3551^2} \approx 0,36\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(S \approx \sqrt {0,36} \approx 0,6\).
