Câu hỏi/bài tập:

Cho đồ thị các hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\), y = x + 1 và hình phẳng được tô màu như hình 30
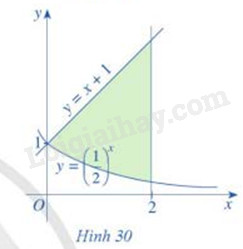
a) Hình phẳng đó được giới hạn bởi các đường nào?
b) Tính diện tích hình phẳng đó
Advertisements (Quảng cáo)

a) Quan sát hình vẽ
b) Cho hàm số y = f(x), y = g(x) liên tục trên đoạn [a;b]. Khi đó, diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b là: \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \)

a) Hình phẳng đó được giới hạn bởi đồ thị hàm số y = x + 1, \(y = {\left( {\frac{1}{2}} \right)^x}\), đường thẳng x = 0 và x = 2
b) Diện tích hình phẳng đó là: \(S = \int\limits_0^2 {\left| {x + 1 - {{\left( {\frac{1}{2}} \right)}^x}} \right|} dx = \int\limits_0^2 {\left( {x + 1 - {{\left( {\frac{1}{2}} \right)}^x}} \right)} dx = \left. {\left( {\frac{{{x^2}}}{2} + x - \frac{{{{\left( {\frac{1}{2}} \right)}^x}}}{{ - \ln 2}}} \right)} \right|_0^2 \approx 2,92\)
