Câu hỏi/bài tập:

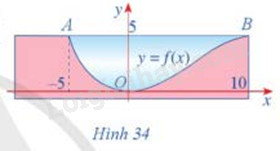
Hình 34 minh họa mặt cắt đứng của một con kênh đặt trong hệ trục tọa độ Oxy. Đáy của con kênh là một đường cong cho bởi phương trình \(y = f(x) = \frac{3}{{100}}\left( { - \frac{1}{3}{x^3} + 5{x^2}} \right)\). Hãy tính diện tích hình phẳng tô màu xanh trong Hình 34, biết đơn vị trên mỗi trục tọa độ là mét

Advertisements (Quảng cáo)
Xác định các đường thẳng giới hạn hình phẳng màu xanh và sử dụng công tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b là: \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \)

Hình phẳng màu xanh được giới hạn bởi đồ thị hàm số y = f(x), đường thẳng y = 5, x = -5 và x =10
Diện tích hình phẳng màu xanh là: \(S = \int\limits_{ - 5}^{10} {\left| {5 - \frac{3}{{100}}\left( { - \frac{1}{3}{x^3} + 5{x^2}} \right)} \right|dx} = \left| {\left( {5x + \frac{{{x^4}}}{{400}} - \frac{{{x^3}}}{{20}}} \right)} \right|_{ - 5}^{10} = \frac{{675}}{{16}}{m^2}\)
