Xét hình tròn tâm O, bán kính r (Hình 24)...

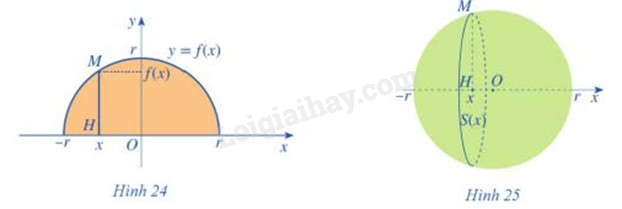
Xét hình tròn tâm O, bán kính r (Hình 24). Nửa hình tròn đó là hình phẳng giới hạn bởi trục Ox và đồ thị hàm số y = f(x)

a) Tìm hàm số y = f(x)

b) Quay nửa hình tròn đó quanh trục hoành, ta nhận được hình cầu tâm O bán kính r (Hình 25). Xét điểm M(x;f(x)) $( - r \le x \le r)$ nằm trên nửa đường tròn tâm O bán kính r. Gọi H(x;0) là hình chiếu của điểm M trên trục Ox. Khi quay nửa hình tròn quanh trục hoành, đoạn thẳng HM tạo nên một hình tròn tâm H bán kính f(x)

Tính diện tích S(x) của hình tròn đó theo f(x)

Từ đó, sử dụng công thức tính thể tích vật thể, hãy tính thể tích V của hình cầu tâm O bán kính r

a) Tìm hàm số y = f(x) thông qua phương trình nửa đường tròn

b) Sử dụng công thức tính thể tích hình cầu

a) Hàm số y = f(x) chính là phương trình của nửa đường tròn có tâm O, bán kính r

$\Rightarrow y = f(x) = \sqrt {{r^2} - {x^2}}$

b) $S(x) = \pi {f^2}(x)$

$V = \frac{{4\pi {r^3}}}{3}$