Câu 1
Viết và đọc phân số chỉ phần đã tô màu của mỗi hình.


Quan sát hình vẽ để viết phân số tương ứng của mỗi hình.

Hình 1: $\frac{1}{7}$: Một phần bảy
Hình 2: $\frac{2}{3}$: Hai phần ba
Hình 3: $\frac{3}{7}$: Ba phần bảy
Hình 4: $\frac{3}{5}$: Ba phần năm
HÌnh 5: $\frac{8}{8}$: Tám phần tám
Câu 2
Viết và đọc các hỗn số chỉ phần đã tô màu của mỗi hình.
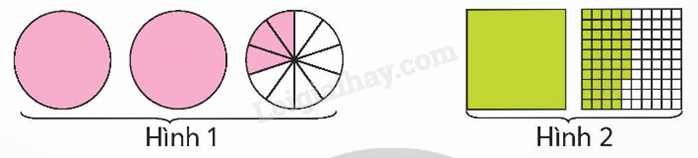

Khi đọc (hoặc viết) hỗn số ta đọc (hoặc viết) phần nguyên rồi đọc (hoặc viết) phần phân số.

Hình 1:
Viết: $2\frac{3}{{10}}$
Đọc: Hai và ba phần mười
Hình 2:
Viết: $1\frac{{47}}{{100}}$
Đọc: Một và bốn mươi bảy phần một trăm
Câu 3
Số?
Trong hình bên:

a) Cái bánh được chia thành .?. phần bằng nhau.
b) Mỗi bạn đã ăn .?. cái bánh
c) Còn lại .?. cái bánh

Quan sát hình và trả lời câu hỏi

a) Cái bánh được chia thành 10 phần bằng nhau.
b) Mỗi bạn đã ăn $\frac{1}{{10}}$ cái bánh
c) Còn lại $\frac{6}{{10}}$ cái bánh
Câu 4
Câu nào đúng, câu nào sai?

Trong hình bên
a) $\frac{5}{4}$ số bạn là nữ
b) $\frac{5}{9}$ số bạn là nữ
c) $\frac{4}{9}$ số bạn là nam
d) $\frac{1}{3}$ số bạn nam đeo kính

Quan sát hình và xác định câu sai, câu đúng.

a) Sai
b) Đúng
c) Đúng
d) Sai
Câu 5
Rút gọn các phân số.
$\frac{6}{{14}};\frac{{15}}{{40}};\frac{{12}}{{18}};\frac{{14}}{{35}};\frac{{140}}{{60}}.$

Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.

$\frac{6}{{14}} = \frac{{6:2}}{{14:2}} = \frac{3}{7}$
$\frac{{15}}{{40}} = \frac{{15:5}}{{40:5}} = \frac{3}{8}$
$\frac{{12}}{{18}} = \frac{{12:6}}{{18:6}} = \frac{2}{3}$
$\frac{{14}}{{35}} = \frac{{14:7}}{{35:7}} = \frac{2}{5}$
$\frac{{140}}{{60}} = \frac{{140:20}}{{60:20}} = \frac{7}{3}$
Câu 6
Quy đồng mẫu số các phân số.
a) $\frac{2}{3}$và $\frac{1}{6}$
b) $\frac{4}{5}$ và $\frac{1}{{15}}$
c) $\frac{5}{{20}}$ và $\frac{{15}}{{12}}$

Khi quy đồng mẫu số hai phân số có thể làm như sau:
- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.

a) Chọn mẫu số chung là 6
Quy đồng mẫu số hai phân số ta có:
$\frac{2}{3} = \frac{{2 \times 2}}{{3 \times 2}} = \frac{4}{6}$; Giữ nguyên phân số $\frac{1}{6}$
Vậy quy đồng mẫu số hai phân số $\frac{2}{3}$ và $\frac{1}{6}$ ta được hai phân số $\frac{4}{6}$ và $\frac{1}{6}$
b) Chọn mẫu số chung là 15
Advertisements (Quảng cáo)
Quy đồng mẫu số hai phân số ta có:
$\frac{4}{5} = \frac{{4 \times 3}}{{5 \times 3}} = \frac{{12}}{{15}}$; Giữ nguyên phân số $\frac{1}{{15}}$
Vậy quy đồng mẫu số hai phân số $\frac{4}{5}$ và $\frac{1}{{15}}$ta được hai phân số $\frac{{12}}{{15}}$ và $\frac{1}{{15}}$
c)
Chọn mẫu số chung là 60
Quy đồng mẫu số hai phân số ta có:
$\frac{5}{{20}} = \frac{{5 \times 3}}{{20 \times 3}} = \frac{{15}}{{60}}$; $\frac{{15}}{{12}} = \frac{{15 \times 5}}{{12 \times 5}} = \frac{{75}}{{60}}$
Vậy quy đồng mẫu số hai phân số $\frac{5}{{20}}$ và $\frac{{15}}{{12}}$ ta được hai phân số $\frac{{15}}{{60}}$ và $\frac{{75}}{{60}}$
Câu 7
> ,
a) $\frac{5}{6}.?.\frac{2}{3}$
$\frac{3}{8}.?.\frac{3}{4}$
$\frac{{10}}{{15}}.?.\frac{{14}}{{21}}$
b) $\frac{5}{7}.?.1$
$\frac{7}{5}.?.1$
$\frac{7}{7}.?.1$

- Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đã cho rồi so sánh hai phân số mới có cùng mẫu số.
- Phân số lớn hơn 1 là phân số có tử số lớn hơn mẫu số.
- Phân số bé hơn 1 là phân số có tử số bé hơn mẫu số.
- Nếu phân số có tử số và mẫu số bằng nhau thì phân số đó bằng 1.

a)
* Ta có: $\frac{2}{3} = \frac{4}{6}$
Mà $\frac{5}{6} > \frac{4}{6}$ nên $\frac{5}{6} > \frac{2}{3}$
* Ta có: $\frac{3}{4} = \frac{6}{8}$
Mà $\frac{3}{8}
* Ta có: $\frac{{10}}{{15}} = \frac{2}{3}$; $\frac{{14}}{{21}} = \frac{2}{3}$
Mà $\frac{2}{3} = \frac{2}{3}$ nên $\frac{{10}}{{15}} = \frac{{14}}{{21}}$
b) $\frac{5}{7}
$\frac{7}{5} > 1$ (vì 7 > 5 )
$\frac{7}{7} = 1$ ( vì 7 = 7 )
Câu 8
Sắp xếp các số sau theo thứ tự từ bé đến lớn.
a) $\frac{1}{3};\frac{1}{4};\frac{5}{{12}};1$
b) $5;\frac{5}{8};\frac{5}{4};\frac{5}{2}$

- Quy đồng mẫu số các phân số rồi so sánh các phân số sau khi quy đồng
- So sánh cùng tử số: Nếu mẫu số của phân số nào bé hơn thì phân số đó lớn hơn và ngược lại.

a) Mẫu số chung là 12
$\frac{1}{3} = \frac{4}{{12}}$; $\frac{1}{4} = \frac{3}{{12}}$; $1 = \frac{{12}}{{12}}$; giữ nguyên phân số $\frac{5}{{12}}$
Ta có: $\frac{3}{{12}}
Vậy các phân số được sắp xếp theo thứ tự từ bé đến lớn là $\frac{1}{4};\frac{1}{3};\frac{5}{{12}};1$
b) Các phân số cùng tử số:
Ta có: $\frac{5}{8}
Vậy các phân số được sắp xếp theo thứ tự từ bé đến lớn là $\frac{5}{8};\frac{5}{4};\frac{5}{2};5$
Câu 9
Phân số?
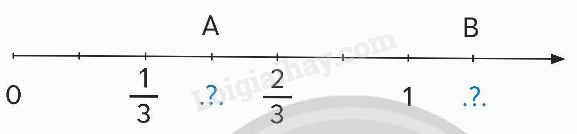

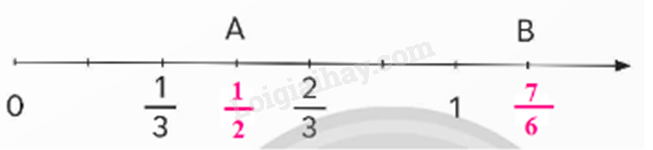
Hai phân số liên tiếp nhau trên tia số hơn kém nhau$\frac{1}{6}$

Vì không có phân số nào có mẫu số là 3 và bé hơn $\frac{1}{3}$, lớn hơn $\frac{2}{3}$
Nên ta có:
$\frac{1}{3} = \frac{2}{6}$; $\frac{2}{3} = \frac{4}{6}$
Vậy phân số ở giữa $\frac{1}{3}$ và $\frac{2}{3}$là $\frac{4}{6} = \frac{1}{2}$
Hai phân số liên tiếp nhau trên tia số hơn kém nhau: $\frac{2}{3}$- $\frac{1}{2}$= $\frac{1}{6}$
Câu 10
Chọn ý trả lời đúng.
Lớp 5A nhận chăm sóc $\frac{2}{5}$số cây trong vườn có nghĩa là:
A. Lớp 5A chăm sóc 2 cây
B. Lớp 5A chăm sóc 5 cây
C. Số cây trong vườn thường được chia đều thành 2 phần, lớp 5A chăm sóc 5 phần.
D. Số cây trong vườn trường được chia đều thành 5 phần, lớp 5A chăm sóc 2 phần.

Dựa kiến thức đã học và trả lời câu hỏi.

Chọn D
Thử thách
Người ta dự định lát nền nhà bằng các viên gạch màu trắng, màu vàng và màu nâu sao cho số viên gạch mỗi màu bằng nhau. Hình dưới đây là hai cách sắp xếp được đề nghị.
a) Cách sắp xếp nào chưa đúng như dự định?
b) Hãy thay đổi màu sắc các viên gạch trong hình đó để có nền nhà như dự định.
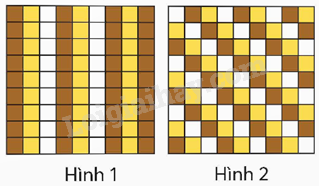

Quan sát hình và trả lời câu hỏi.

a) Cách xếp hình 1 chưa đúng như dự định vì màu nâu được xếp nhiều hơn.
b) Thay đổi 1 hàng dọc viên gạch màu nâu (9 viên) thành màu trắng
