Chọn câu trả lời đúng.
Chiếc hộp nào dưới đây có diện tích toàn phần lớn nhất?
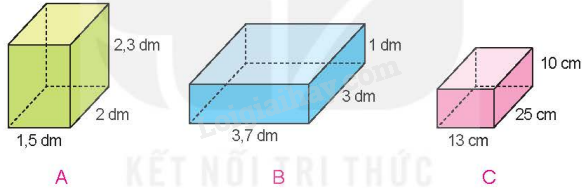

- Tính diện tích toàn phần của từng chiếc hộp
- So sánh diện tích toàn phần của từng chiếc hộp và chọn chiếc hộp có diện tích toàn phần lớn nhất.
- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.

Hình A.
Diện tích xung quanh của chiếc hộp là:
(2 + 1,5) x 2 x 2,3 = 16,1 (dm2)
Diện tích hai đáy của hình hộp chữ nhật là:
2 x 1,5 x 2 = 6 (dm2)
Diện tích toàn phần của hình hộp chữ nhật là:
16,1 + 6 = 22,1 (cm2)
Hình B.
Advertisements (Quảng cáo)
Diện tích xung quanh của chiếc hộp là:
(3,7 + 3) x 2 x 1 = 13,4 (dm2)
Diện tích hai đáy của hình hộp chữ nhật là:
3,7 x 3 x 2 = 22,2 (dm2)
Diện tích toàn phần của hình hộp chữ nhật là:
13,4 + 22,2 = 35,6 (dm2)
Hình C.
Diện tích xung quanh của chiếc hộp là:
(25 + 13) x 2 x 10 = 760 (cm2)
Diện tích hai đáy của hình hộp chữ nhật là:
25 x 13 x 2 = 650 (cm2)
Diện tích toàn phần của hình hộp chữ nhật là:
760 + 650 = 1 410 (cm2)
Đổi: 1 410 cm2 = 14,1 dm2
Ta có: 14,1 dm2 < 22,1 dm2 < 35,6 dm2
Vậy chiếc hộp B có diện tích toàn phần lớn nhất.
Chọn B.
