
Trong Hình 3 cho biết a // b. Tìm số đo các góc đỉnh A và B.
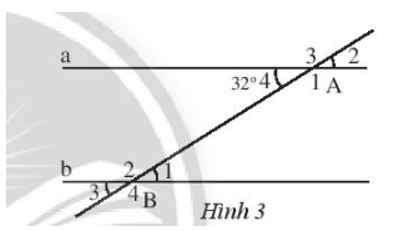

Ta sử dụng tính chất 2 góc so le trong để tính góc B1 sau đó dùng tính chất 2 góc kề bù và 2 góc đối đỉnh để tính lần lượt các góc đỉnh B

– Tại đỉnh A:
• Vì \(\widehat {{A_2}}\)và \(\widehat {{A_4}}\) là hai góc đối đỉnh nên \(\widehat {{A_2}}\)=\(\widehat {{A_4}}\)=32°.
• Vì \(\widehat {{A_1}}\) và \(\widehat {{A_4}}\) là hai góc kề bù nên ta có:
Advertisements (Quảng cáo)
\(\widehat {{A_1}}\)+\(\widehat {{A_4}}\)=180°
Suy ra \(\widehat {{A_1}}\)=180°−\(\widehat {{A_4}}\)=180°−32°=148°
• Vì \(\widehat {{A_1}}\) và \(\widehat {{A_3}}\) là hai góc đối đỉnh nên \(\widehat {{A_1}}\)=\(\widehat {{A_3}}\)=148°.
– Tại đỉnh B:
Vì a // b nên:
• \(\widehat {{B_1}}\)=\(\widehat {{A_4}}\)=32° (hai góc so le trong)
• \(\widehat {{B_2}}\)=\(\widehat {{A_1}}\)=148° (hai góc so le trong)
• \(\widehat {{B_3}}\)=\(\widehat {{A_4}}\)=32° (hai góc đồng vị)
• \(\widehat {{B_4}}\)=\(\widehat {{A_1}}\)=148° (hai góc đồng vị).
Vậy \(\widehat {{B_1}}\)=32°,\(\widehat {{B_2}}\)=148°,\(\widehat {{B_3}}\)=32°,\(\widehat {{B_4}}\)=148°.
