
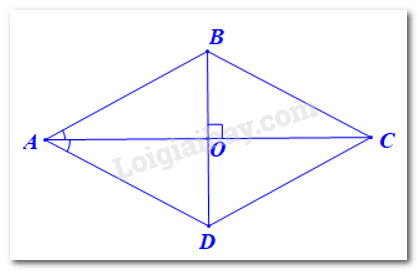
Cho hình thoi ABCD, biết AC là phân giác \(\widehat {BAD}\). Hãy chứng tỏ CA là phân giác \(\widehat {BCD}\).

Sử dụng tính chất của hình thoi có các cặp đối diện song song và bằng nhau. Sau khi đã chọn được cặp cạnh song song, ta sử dụng tính chất 2 góc so le trong bằng nhau để suy ra \(\widehat {DCA}\)=\(\widehat {ACB}\) nên CA là phân giác của \(\widehat {BCD}\)

Advertisements (Quảng cáo)
Vì ABCD là hình thoi nên AB // CD và AD // BC.
Do AB // CD nên \(\widehat {BAC}\)=\(\widehat {DCA}\) (hai góc so le trong)
Do AD // BC nên \(\widehat {CAD}\)=\(\widehat {ACB}\) (hai góc so le trong)
Mà AC là tia phân giác của \(\widehat {BAD}\) nên \(\widehat {BAC}\)=\(\widehat {CAD}\)
Suy ra \(\widehat {DCA}\)=\(\widehat {ACB}\)
Mà tia CA nằm giữa 2 tia CB và CD
Do đó CA là tia phân giác của \(\widehat {BCD}\)
