Bài 4.45 trang 69 SBT Toán 7 Kết nối tri thức: Cho ABC là tam giác cân tại đỉnh A. Chứng minh rằng:...

Cho ABC là tam giác cân tại đỉnh A. Chứng minh rằng:

a) Hai đường trung tuyến BM, CN bằng nhau (H.4.50a).

b) Hai đường phân giác BE, CF bằng nhau (H.4.50b) 

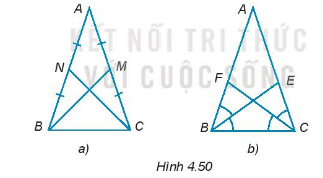
a)Chứng minh $\Delta ABM = \Delta ACM\left( {c - g - c} \right)$

b)Chứng minh: $\Delta ABE = \Delta ACF\left( {g - c - g} \right)$

a) Ta có: $AM = \dfrac{{AC}}{2}; AN=\dfrac{{AB}}{2}$.

Mà tam giác ABC cân tại A nên AB = AC.

$\Rightarrow AM=AN$

Xét $\Delta ABM$ và $\Delta ACM$ có:

AB = AC

$\begin{array}{l}AM = AN\\\widehat A:Chung\\ \Rightarrow \Delta ABM = \Delta ACM\left( {c - g - c} \right)\\ \Rightarrow BM = CN\end{array}$

b) Ta có: $\widehat {ABE} = \dfrac{{\widehat {ABC}}}{2}$ (do BE là tia phân giác của góc ABC)

$\widehat {ACF}= \dfrac{{\widehat {ACB}}}{2}$ (do CF là tia phân giác của góc ACB)

Mà tam giác ABC cân tại A nên $\widehat {ABC}=\widehat {ACB}$

Do đó, $\widehat {ABE} = \widehat {ACF}$

Xét $\Delta ABE$ và $\Delta ACF$ có:

$\widehat A:Chung\\AB=AC\\\widehat {ABE} = \widehat {ACF}\\ \Rightarrow \Delta ABE = \Delta ACF\left( {g - c - g} \right)$

$\Rightarrow BE = CF.$ ( 2 cạnh tương ứng)