
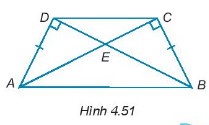
Cho các điểm A, B, C, D, E như Hình 4.51. Chứng minh rằng:
a) \(\Delta AEB,\Delta DEC\) là các tam giác cân đỉnh E.
b) \(AB\parallel CD.\)

a)
-Chứng minh: \(\Delta ADB = \Delta BCA\left( {ch - cgv} \right)\)
- Chứng minh: \(\Delta ADC = \Delta BCD\left( {c - g - c} \right)\)
b) Chứng minh \(\widehat {ABD} = \widehat {CDB}\).
Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.

a)
- Xét \(\Delta ADB\) và \(\Delta BCA\) có:
\(\widehat {ADB} = \widehat {BCA} = {90^0}\\AD = BC\left( {gt} \right)\\AB:Chung\\ \Rightarrow \Delta ADB = \Delta BCA\left( {ch - cgv} \right)\)
\( \Rightarrow \widehat {ABD} = \widehat {BAC}\) ( 2 góc tương ứng)
Advertisements (Quảng cáo)
Hay \(\widehat {EAB} = \widehat {EBA}\)
\( \Rightarrow \Delta AEB\) cân tại đỉnh E.
Vì \(\Delta ADB = \Delta BCA \Rightarrow BD = AC,\widehat {DAB} = \widehat {CBA}\)
Lại có: \(\widehat {DAC} = \widehat {DAB} - \widehat {CAB} = \widehat {CBA} - \widehat {ABD} = \widehat {CBD}\)
- Xét \(\Delta ADC\) và \(\Delta BCD\) có:
AD = BC
AC = BD
\(\widehat {DAC} = \widehat {CBD}\)
\( \Rightarrow \Delta ADC = \Delta BCD\left( {c - g - c} \right)\)
\(\Rightarrow \widehat {DCA} = \widehat {CDB}\) (2 góc tương ứng)
Hay \(\widehat {DCE} = \widehat {CDE}\)
Vậy tam giác DEC cân tại E.
b)
Ta có:
\(\begin{array}{l}\widehat {ABD} = \widehat {ABE} = \dfrac{{\widehat {ABE} + \widehat {BAE}}}{2} = \dfrac{{{{180}^0} - \widehat {AEB}}}{2} = \dfrac{{{{180}^0} - \widehat {DEC}}}{2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\widehat {DCE} + \widehat {CDE}}}{2} = \widehat {CDE} = \widehat {CDB}\end{array}\)
Mà 2 góc \(\widehat{ABD}\) và \(\widehat{CDB}\) ở vị trí so le trong
Vậy \(AB// CD\) (Dấu hiệu nhận biết 2 đường thẳng song song)
