
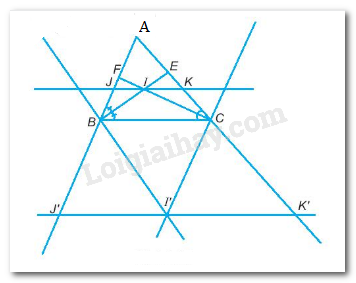
a)Gọi I là giao điểm của hai đường phân giác BE và CF của tam giác ABC. Đường thẳng qua I song song với BC cắt AB tại J và cắt AC tại K. Chứng minh: JK = BJ + CK.
b)Đường thẳng qua B vuông góc với BI cắt đường thẳng qua C vuông góc với CI tại điểm I’. Qua I’ kẻ đường thẳng song song với BC cắt AB tại J’, cắt AC tại K’. Chứng minh J’K’ = BJ’ + CK’.

a)Chứng minh tam giác JIB cân tại J, tam giác IKC cân tại K
b)Áp dụng: 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
BI vuông góc BI’ suy ra BI’ là phân giác góc ngoài tại B

a)
Ta có: BI là phân giác góc FBC
\( \Rightarrow \widehat {JBI} = \widehat {IBC}\)
Lại có: JK // BC
\( \Rightarrow \widehat {JIB} = \widehat {IBC}\)(2 góc so le trong)
\( \Rightarrow \widehat {JBI} = \widehat {JIB}\)\(\)
Advertisements (Quảng cáo)
\( \Rightarrow \Delta JIB\)cân tại J
\( \Rightarrow JI = JB\)
Chứng minh tương tự: KI = KC
Ta có:
\(JK = JI + IK = JB + CK\)
b)
Ta có: \(BI’ \bot BI\)
\( \Rightarrow BI’\) là tia phân giác của góc tạo bởi BC và tia đối của tia BA (phân giác góc ngoài tại B)
\( \Rightarrow \widehat {J’BI’} = \widehat {I’BC}\) (Tính chất tia phân giác)
Lại có: BC // J’K’
\( \Rightarrow \widehat {CBI’} = \widehat {BI’J’}\) (2 góc so le trong)
\( \Rightarrow \widehat {J’BI’} = \widehat {BI’J’}\)
\( \Rightarrow \Delta J’BI’\) cân tại J’
\( \Rightarrow J’B = J’I’\)
Chứng minh tương tự: K’C = K’I’
Ta có:
J’K’ = J’I’ + I’K’ = BJ’ + CK’ (đpcm)
