Giải bài 9.24 trang 76 SGK Toán lớp 7 tập 2 Kết nối tri thức với cuộc sống - Bài 34: Sự đồng quy của ba đường trung tuyến - ba đường phân giác trong một tam giác
![]()
Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh BE = CF.
![]()
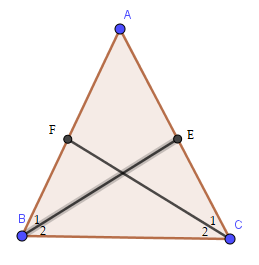
Vì tam giác ABC cân tại A nên AB = AC; \(\widehat {ABC} = \widehat {ACB}\) ( tính chất)
Vì BE là là tia phân giác của góc ABC nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}.\widehat {ABC}\)
Vì CF là tia phân giác của góc ACB nên \(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}.\widehat {ACB}\)
Advertisements (Quảng cáo)
Do đó, \(\widehat {{B_1}} = \widehat {{C_1}}\)
Xét \(\Delta ABE\) và \(\Delta ACF\), ta có:
\(\widehat A\) chung
AB = AC
\(\widehat {{B_1}} = \widehat {{C_1}}\)
\( \Rightarrow \Delta ABE = \Delta ACF\left( {g.c.g} \right)\)
\( \Rightarrow \)BE = CF ( 2 cạnh tương ứng)
