Giải Bài 9.18 trang 55 sách bài tập toán 7 - Kết nối tri thức với cuộc sống - Bài 34. Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác

Cho tam giác ABC với M là trung điểm của BC. Lấy điểm N sao cho C là trung điểm của đoạn thẳng BN. Lấy điểm P sao cho M là trung điểm của đoạn thẳng AP. Chứng minh đường thẳng AC đi qua trung điểm của PN, đường thẳng PC đi qua trung điểm của AN.

Chứng minh CM = 2CN
Từ đó suy ra: C là trọng tâm tam giác APN

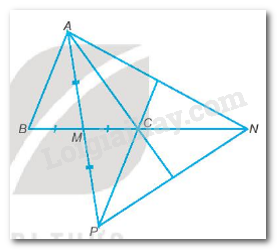
Ta có:
Advertisements (Quảng cáo)
M là trung điểm BC nên BM = CM = \(\dfrac{1}{2}BC\)
\( \Rightarrow BC = 2CM\)
C là trung điểm BN nên BC = CN
\( \Rightarrow CN = 2CM\)
Xét tam giác ANP có NM là đường trung tuyến
Mà: CN = 2CM (cmt)
\( \Rightarrow \) C là trọng tâm tam giác ANP
\( \Rightarrow \) AC, PC là hai tiếp tuyến của tam giác đó
\( \Rightarrow \) AC đi qua trung điểm của PN
PC đi qua trung điểm của AN.
