
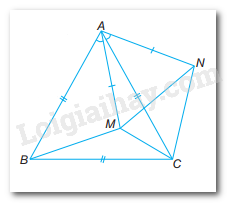
Cho M là một điểm tuỳ ý bên trong tam giác đều ABC. Lấy điểm N nằm khác phía với M đối với đường thẳng AC sao cho \(\widehat {CAN} = \widehat {BAM}\) và AN = AM.
Chứng minh:
a) Tam giác AMN là tam giác đều
b) \(\Delta MAB = \Delta NAC\)
c) MN = MA, NC = MB

a)Tam giác AMN cân có 1 góc bằng 60 độ
b) Cm: \(\Delta MAB = \Delta NAC\) (c – g – c )
c) Áp dụng ý a, b.

a)
Tam giác ABC là tam giác đều nên: \(\widehat A = \widehat B = \widehat C = {60^0}\)
Advertisements (Quảng cáo)
Ta có:
\(\begin{array}{l}\widehat {MAN} = \widehat {MAC} + \widehat {CAN} = \widehat {MAC} + \widehat {BAM}\left( {do\,\,\widehat {CAN} = \widehat {BAM}} \right)\\ \Rightarrow \widehat {MAN} = \widehat {BAC} = {60^0}\end{array}\)
Xét tam giác AMN có: AM = AN (gt)
\( \Rightarrow \Delta AMN\) cân tại A
Mà \(\widehat {MAN} = {60^0} \Rightarrow \Delta ABC\) là tam giác đều.
b)
Xét \(\Delta MAB\) và \(\Delta NAC\) có:
AB = AC (gt)
AM = AN (gt)
\(\widehat {MAB} = \widehat {NAC}\)(gt)
\( \Rightarrow \)\(\Delta MAB\)= \(\Delta NAC\) (c – g – c)
c)
Tam giác AMN đều (cm ý a)
\( \Rightarrow \)MN = MA
\(\Delta MAB\)= \(\Delta NAC\) (cm ý b)
\( \Rightarrow MB = NC\)(cạnh tương ứng)
