1.
Tìm phương án Sai trong câu sau: Trong tam giác
A.đối diện với góc lớn nhất là cạnh lớn nhất
B.đối diện với cạnh bé nhất là góc nhọn
C.đối diện với cạnh lớn nhất là góc tù
D.đối diện với góc tù (nếu có) là cạnh lớn nhất.

Quan hệ giữa góc và cạnh đối diện trong một tam giác

Chọn C
2.
Bộ ba số nào sau đây không là độ dài ba cạnh của một tam giác?
|
A.7, 5, 7 |
B.7, 7, 7 |
C.3, 5, 4 |
D.4, 7, 3 |

Áp dụng bất đẳng thức tam giác
Nếu cạnh lớn nhất nhỏ hơn tổng 2 cạnh còn lại thì bộ ba số có là độ dài ba cạnh của một tam giác.

4 + 3 = 7 => Bộ ba số 4,7,3 không là độ dài ba cạnh của một tam giác.
Chọn D
3.
Tam giác cân có độ dài cạnh bên b, độ dài cạnh đáy d thì ta phải có:
|
A.d > b |
B.d = 2b |
C.d < b/2 |
D. d < 2b |

Áp dụng bất đẳng thức tam giác
Trong tam giác cân, 2 cạnh bên bằng nhau

Tam giác có 2 cạnh bên là b, áp dụng bất đẳng thức trong tam giác:
b + b > d => 2b > d.
Chọn D
4.
Với mọi tam giác ta đều có:
A.mỗi cạnh lớn hơn nửa chu vi
B.mỗi cạnh lớn hơn hoặc bằng nửa chu vi
Advertisements (Quảng cáo)
C.mỗi cạnh nhỏ hơn nửa chu vi
D.cả ba trường hợp trên đều có thể xảy ra.

Áp dụng bất đẳng thức tam giác

Ba cạnh bất kì trong tam giác:a, b, c
Theo bất đẳng thức tam giác: a < b + c =>a + a < a + b + c
Vậy mỗi cạnh nhỏ hơn nửa chu vi.
5.
Xét hai đường trung tuyến BM, CN của tam giác ABC có BC = 4cm. Trong các số sau, số nào có thể là tổng độ dài BM + CN?
|
A.5 cm |
B.5,5 cm |
C.6 cm |
D.6,5 cm |

Áp dụng bất đẳng thức tam giác
Tính chất trọng tâm tam giác

G là trọng tâm tam giác ABC
Xét tam giác GBC có GB + GC > BC ( Bất đẳng thức tam giác)
\(\begin{array}{l} \Rightarrow \dfrac{2}{3}\left( {BM + CN} \right) > BC\\ \Rightarrow BM + CN > \dfrac{3}{2}BC = 6\end{array}\)
Chọn D.
6.
Tam giác ABC có số đo ba góc thoả mãn: \(\widehat A = \widehat B + \widehat C\). Hai tia phân giác của góc A và góc B cắt nhau tại điểm I. Khi đó góc BIC có số đo là:
|
A.\({120^0}\) |
B. \({125^0}\) |
C. \({130^0}\) |
D. \({135^0}\) |

Áp dụng định lí về tổng ba góc trong tam giác; tính chaasrt tia phân giác của một góc.

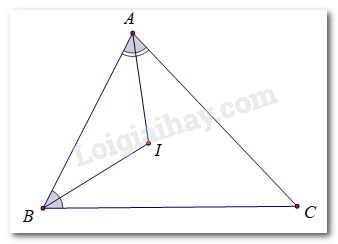
Ta có:
\(\widehat A + \widehat B + \widehat C = {180^0}\)(Tổng ba góc trong tam giác)
Mà \(\widehat A = \widehat B + \widehat C\)
\(\begin{array}{l} \Rightarrow \left( {\widehat B + \widehat C} \right) + \widehat B + \widehat C = {180^0}\\ \Rightarrow 2\left( {\widehat B + \widehat C} \right) = {180^0}\\ \Rightarrow \widehat B + \widehat C = {180^0}:2 = {90^0}\\ \Rightarrow \widehat A = \widehat B + \widehat C = {90^0}\end{array}\)
Xét tam giác BIC có:
\(\widehat {BIC} = {180^0} - \left( {\widehat {\dfrac{B}{2}} + \dfrac{{\widehat C}}{2}} \right) = {180^0} - \dfrac{{{{90}^0}}}{2} = {180^0} - {45^0} = {135^0}\).
Chọn D.
