
Cho C là trung điểm của đoạn thẳng AB. Gọi Ax, By là hai đường thẳng vuông góc với AB tại A và tại B. Một đường thẳng qua C cắt Ax tại M, cắt By tại P. Điểm N nằm trên tia đối của tia BP sao cho góc MCN là góc vuông. Gọi H là hình chiếu của C trên MN.
Chứng minh:
a)AM + BN = MN;
b) CM là đường trung trực của AH, CN là đường trung trực của BH;
c) Góc AHB là góc vuông.

a)
-Chứng minh AM = MH: \(\Delta AMC = \Delta HMC\)
-Chứng minh:NB = NH:\(\Delta CHN = \Delta CBN\left( {ch - gn} \right)\)
b)Áp dụng kết quả ý a
c)Trong tam giác đường trung tuyến ứng với 1 cạnh và bằng nửa cạnh đó thì tam giác đó là tam giác vuông

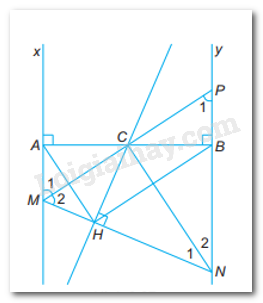
a)
-Chứng minh AM = MH
Xét \(\Delta AMC\) và \(\Delta BPC\) có:
AC = CB (gt)
\(\widehat {MAC} = \widehat {PBC} = {90^0}\)
\(\widehat {ACM} = \widehat {BCP}\)(đối đỉnh)
\( \Rightarrow \)\(\Delta AMC\) = \(\Delta BPC\)(g – c – g)
\( \Rightarrow \) MC = CP (cạnh tương ứng)
Mà \(NC \bot MP\)
Advertisements (Quảng cáo)
\( \Rightarrow \)NC là đường trung trực của MP
\( \Rightarrow \)Tam giác NMP cân tại N
\( \Rightarrow \)\(\widehat {{P_1}} = \widehat {{M_2}}\)
Mà \(\widehat {{P_1}} = \widehat {{M_1}}\)(so le trong: Mx // By)
\( \Rightarrow \widehat {{M_1}} = \widehat {{M_2}}\)
Xét \(\Delta AMC\) và \(\Delta HMC\) có:
\(\begin{array}{l}\widehat {MAC} = \widehat {MHC} = {90^0}\\MC:chung\\\widehat {{M_1}} = \widehat {{M_2}}\left( {cmt} \right)\\ \Rightarrow \Delta AMC = \Delta HMC\left( {ch - gn} \right)\\ \Rightarrow AM = MH\left( {ctu} \right)\end{array}\)
-Chứng minh:NB = NH
Tam giác MNP cân tại N có NC là đường trung trực đồng thời là đường phân giác xuất phát từ N.
Xét \(\Delta HNC\) và \(\Delta BNC\) có:
CN: chung
\(\begin{array}{l}\widehat {{N_1}} = \widehat {{N_2}}\left( {cmt} \right)\\\widehat {CHN} = \widehat {CBN} = {90^0}\\ \Rightarrow \Delta CHN = \Delta CBN\left( {ch - gn} \right)\end{array}\)\( \Rightarrow NH = NB\)(cạnh tương ứng)
\( \Rightarrow AM + BN = MH + HN = MN\)
b)
Tam giác MAH cân tại M với MC là đường phân giác xuất phát từ đỉnh cân M
\( \Rightarrow \)MC là đồng thời là đường trung trực của AH
Tam giác NBH cân tại N với NC là đường phân giác xuất phát từ đỉnh cân N
\( \Rightarrow \)NC đồng thời là đường trung trực của BH.
c)
Xét tam giác HAB có CA = CB
\( \Rightarrow \)HC là đường trung tuyến
\(\Delta AMC = \Delta HMC\)(cmt) \( \Rightarrow AC = HC\)(cạnh tương ứng)
\( \Rightarrow HC = CA = CB\)
Đường trung tuyến ứng với cạnh AB và bằng nửa cạnh AB.
Vậy tam giác HAB vuông tại H.
