Giải bài 4 trang 119 SGK Toán 7 tập 2 - Cánh diều - Bài tập cuối chương VII

Cho hai tam giác ABC và MNP có: AB = MN, BC = NP, CA = PM. Gọi I và K lần lượt là trung điểm của BC và NP. Chứng minh AI = MK.

Chứng minh AI = MK bằng cách chứng hai tam giác ABI và MNK bằng nhau.

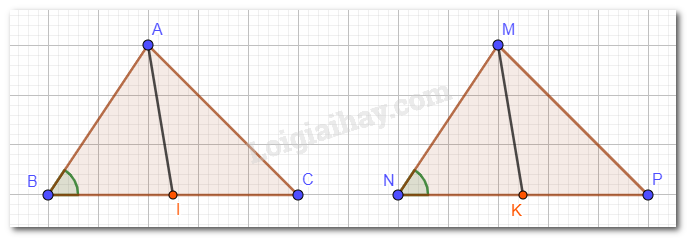
Hai tam giác ABC và MNP có: AB = MN, BC = NP, CA = PM nên \(\Delta ABC = \Delta MNP\)(c.c.c)
Advertisements (Quảng cáo)
Suy ra: \(\widehat {ABI} = \widehat {MNK}\) ( 2 góc tương ứng).
Ta có: I, K lần lượt là trung điểm của BC và NP mà BC = NP, suy ra: \(BI = NK\).
Xét tam giác ABI và tam giác MNK có:
AB = MN;
\(\widehat {ABI} = \widehat {MNK}\);
BI = NK.
Vậy \(\Delta ABI = \Delta MNK\)(c.g.c). Suy ra: AI = MK (2 cạnh tương ứng).
Vậy AI = MK.
