
Cho Hình 142 có O là trung điểm của đoạn thẳng AB và O nằm giữa hai điểm M, N. Chứng minh:
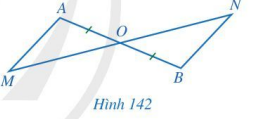
a) Nếu OM = ON thì AM // BN;
b) Nếu AM // BN thì OM = ON.

Chứng minh dựa vào chứng minh hai tam giác AOM và BON bằng nhau.

a) Xét tam giác AOM và tam giác BON có:
OA = OB;
Advertisements (Quảng cáo)
\(\widehat {AOM} = \widehat {BON}\)(đối đỉnh);
OM = ON.
Vậy \(\Delta AOM = \Delta BON\)(c.g.c).
Suy ra: \(\widehat {AMO} = \widehat {BNO}\) (2 góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AM // BN.
b) Ta có: AM // BN nên \(\widehat {MAO} = \widehat {NBO}\)(hai góc so le trong).
Xét tam giác AOM và tam giác BON có:
\(\widehat {MAO} = \widehat {NBO}\)
OA = OB;
\(\widehat {AOM} = \widehat {BON}\)(đối đỉnh);
Vậy \(\Delta AOM = \Delta BON\)(g.c.g). Suy ra: OM = ON ( 2 cạnh tương ứng).
