Hướng dẫn giải bài 5 trang 35 SGK Toán 7 Cánh diều tập 1. Bài 1: Số vô tỉ. Căn bậc hai số học - Chương 2 Số thực
![]()
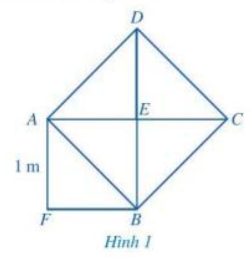
Quan sát Hình 1, ở đó hình vuông AEBF có cạnh bằng 1 dm, hình vuông ABCD có cạnh AB là một đường chéo của hình vuông AEBF.
a) Tính diện tích của hình vuông ABCD.
b) Tính độ dài đường chéo AB.
Lưu ý: √2 là độ dài đường chéo của hình vuông có độ dài cạnh bằng 1.
![]()
a) Quan sát Hình 1 ta thấy hình vuông ABCD được tạo thành từ 4 tam giác nhỏ bằng nhau nên diện tích hình vuông ABCD gấp 4 lần diện tích tam giác AEB.
Hình vuông AEBF là hình vuông có cạnh bằng 1 và tạo bởi hai tam giác là AEB và AFB nên diện tích của hình vuông AEBF gấp 2 lần diện tích của tam giác AEB.
Advertisements (Quảng cáo)
Diện tích hình vuông AEBF có cạnh bằng 1 m là: 1.1 = 1 (dm2).
Diện tích hình vuông AEBF gấp 2 lần diện tích tam giác AEB nên diện tích tam giác AEB là:
![]()
Diện tích hình vuông ABCD gấp 4 lần diện tích tam giác AEB nên diện tích hình vuông ABCD là:
![]()
Vậy diện tích hình vuông ABCD là 2 dm2.
b) Do √2 là độ dài đường chéo của hình vuông có độ dài cạnh bằng 1, mà hình vuông AEBF có cạnh bằng 1 dm nên đường chéo AB là √2 dm.
Vậy độ dài đường chéo AB là √2 dm.
