II. Quan hệ giữa đường vuông góc và đường xiên
HĐ
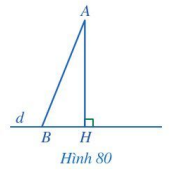
Giả sử AH, AB lần lượt là đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng d (Hình 80). Trong tam giác AHB, hãy so sánh:
a) Số đo góc AHB và số đo góc ABH;
b) Độ dài cạnh AB và độ dài cạnh AH.

a) Tổng ba góc trong một tam giác bằng 180°.
b) Cạnh đối diện với góc lớn hơn thì có độ dài lớn hơn.

a) Tổng ba góc trong một tam giác bằng 180°. Mà góc H bằng 90° nên tổng hai góc còn lại trong tam giác bằng \(180^\circ - 90^\circ = 90^\circ \).
Vậy \(\widehat {AHB} > \widehat {ABH}\).
Advertisements (Quảng cáo)
b) Cạnh đối diện với góc lớn hơn thì có độ dài lớn hơn. Vậy AB > AH (AB đối diện với góc H; AH đối diện với góc B).
LT - VD 2
Cho tam giác nhọn ABC, \(\widehat B > \widehat C\). Gọi H là hình chiếu của A lên BC. Sắp xếp các đoạn thẳng AB, AH, AC theo thứ tự độ dài tăng dần.

Trong một tam giác, đường vuông góc luôn nhỏ hơn đường xiên.
Trong một tam giác, cạnh đối diện với góc lớn hơn thì có độ dài lớn hơn.

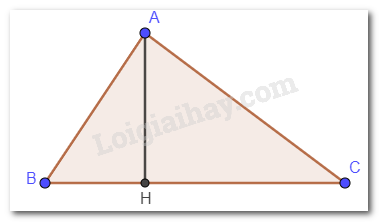
Xét tam giác ABC có: H là hình chiếu của A lên BC nên \(AH \bot BC\). Vậy AH < AB, AC.
Mà trong tam giác ABC có \(\widehat B > \widehat C\)nên AC > AB (AC đối diện với góc B; AB đối diện với góc C).
Các đoạn thẳng AB, AH, AC theo thứ tự độ dài tăng dần là: AH, AB, AC.
