Lời giải bài 2 trang 66 SGK Toán 7 tập 2 – Chân trời sáng tạo – Bài 4. Đường vuông góc và đường xiên
Cho tam giác ABC có \(\widehat A = \)\({100^0}\),\(\widehat B\)\( = {40^o}\).
a) Tìm cạnh lớn nhất của tam giác ABC.
b) Tam giác ABC là tam giác gì? Vì sao?
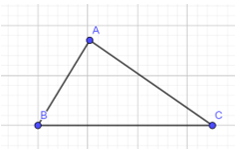
– Sử dụng định lí về góc đối diện cạnh trong tam giác
– Sử dụng tính chất tam giác cân
a) Theo định lí tổng 3 góc trong tam giác, ta có:
\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat C = {180^o} – {100^o} – {40^o} = {40^o}\)
\( \Rightarrow \widehat A > \widehat C\) và \(\widehat A > \widehat B\)
\( \Rightarrow \) BC là cạnh lớn nhất của tam giác ABC do đối diện với góc A
b) Xét tam giác ABC có:
\(\widehat C = \widehat B = {40^o}\)( chứng minh a )
\( \Rightarrow \) ABC là tam giác cân