HĐ 2
Vẽ một tam giác rồi dùng êke vẽ ba đường cao của tam giác ấy (Hình 3). Em hãy quan sát và cho biết các đường cao vừa vẽ có cùng đi qua một điểm hay không.

- Ta sử dụng êke vẽ 3 đường cao của tam giác
- Sau đó nhận xét về các giao điểm của những đường cao ấy

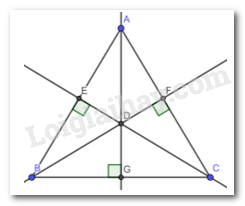
Nhận xét: Các đường cao cùng đi qua 1 điểm
Thực hành 2
Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6). Chứng minh rằng NS vuông góc với ML.

- Ta sử dụng định lí 3 đường cao của một tam giác cùng đi qua 1 điểm

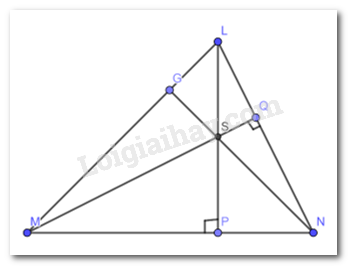
Theo giả thiết ta có : LP và MQ là 2 đường cao của tam giác
Chúng cắt nhau tại S
Theo định lí 3 đường cao trong 1 tam giác cùng đi qua 1 điểm
\( \Rightarrow \)Đường cao từ đỉnh N cũng đi qua S
\( \Rightarrow \)NS là đường cao của tam giác MNL
\( \Rightarrow \) NS vuông góc với ML tại G (là chân đường cao)
Vận dụng 2
Cho tam giác ABC có ba đường cao AD, BE, CF đồng qui tại trực tâm H. Tìm trực tâm của các tam giác HBC, HAB, HAC.
Advertisements (Quảng cáo)

- Từ các đỉnh ta vẽ các đường cao của tam giác chúng giao nhau ở đâu thì đó là trực tâm

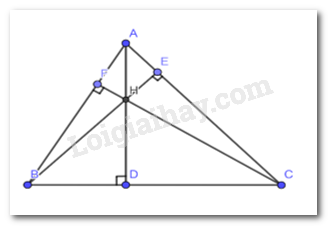
+) Xét tam giác HBC ta có :
HD vuông góc với BC \( \Rightarrow \) HD là đường cao tam giác HBC
BF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)BF là đường cao của tam giác HBC
CE vuông góc với HB tại E ( kéo dài HB ) \( \Rightarrow \)CE là đường cao của tam giác HBC
Ta kéo dài HD, BF, CE sẽ cắt nhau tại A
\( \Rightarrow \) A là trực tâm tam giác HBC
+) Xét tam giác HAB ta có :
HF vuông góc với AB \( \Rightarrow \) HF là đường cao tam giác HAB
BH vuông góc với AE tại E ( kéo dài HB ) \( \Rightarrow \)AE là đường cao của tam giác HAB
BD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)BD là đường cao của tam giác HAB
Ta kéo dài HF, BD, AE sẽ cắt nhau tại C
\( \Rightarrow \) C là trực tâm tam giác HAB
+) Xét tam giác HAC ta có :
HE vuông góc với AC \( \Rightarrow \) HE là đường cao tam giác HAC
AF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)AF là đường cao của tam giác HAC
CD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)CD là đường cao của tam giác HAC
Ta kéo dài CD, HE, AF sẽ cắt nhau tại B
\( \Rightarrow \) B là trực tâm tam giác HAC.
