
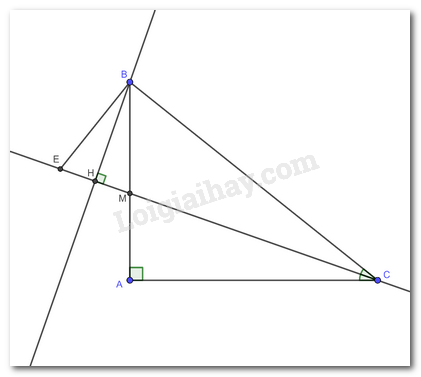
Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB ở M. Từ B kẻ BH vuông góc với đường thẳng CM (H ∈ CM). Trên tia đối của tia HC lấy điểm E sao cho HE = HM.
a) Chứng minh rằng tam giác MBE cân.
b) Chứng minh rằng \(\widehat {EBH} = \widehat {ACM}\)
c) Chứng minh rằng \(EB \bot BC\)

a)Ta chứng minh \(\Delta \)BME có 2 cạnh bên hoặc 2 góc đáy bằng nhau thông qua việc chứng minh 2 tam giác EHB và MHB bằng nhau.
b)Ta chứng minh \(\widehat {EBH} = \widehat {ACM}\)do cùng = \(\widehat {MBH}\)
c)Ta chứng minh\(\widehat {EBH} + \widehat {BCE} = {90^o}\)

a)Xét \(\Delta \)BHE và \(\Delta \)BHM có :
BH là cạnh chung
EH = HM (do M đối xứng E qua H)
Advertisements (Quảng cáo)
\(\widehat {BHE} = \widehat {BHM} = {90^o}\)
\( \Rightarrow \)\(\Delta \)BHE = \(\Delta \)BHM (c-g-c)
\( \Rightarrow \)BM = BE (cạnh tương ứng)
và \(\widehat {EBH} = \widehat {MBH}\)(góc tương ứng) (1)
\( \Rightarrow \)\(\Delta \)BEM cân tại B (2 cạnh bên bằng nhau)
b)Xét \(\Delta \)BHM vuông tại H \( \Rightarrow \widehat {BMH} + \widehat {MBH} = {90^o}\)
Xét \(\Delta \)AMC vuông tại A \( \Rightarrow \widehat {AMC} + \widehat {MCA} = {90^o}\)
Mà \(\widehat {HMB} = \widehat {AMC}\)(2 góc đối đỉnh)
\( \Rightarrow \widehat {MCA} = \widehat {MBH} = {90^o} - \widehat {AMC} = {90^o} - \widehat {HMB}\)(2)
Từ (1) và (2) \( \Rightarrow \widehat {EBH} = \widehat {ACM}\)
c)Vì \(\widehat {BCM} = \widehat {ACM}\) (do CM là phân giác góc C)
\( \Rightarrow \widehat {EBH} = \widehat {BCM}\)(cùng bằng \(\widehat {AMC}\)) (3)
Xét \(\Delta \)EHB vuông tại H có \(\widehat {EBH} + \widehat {BEH} = {90^o}\)(4)
Từ (3) và (4) \( \Rightarrow \widehat {BMC} + \widehat {BEH} = {90^o}\)
\( \Rightarrow \widehat {EBC} = {90^o} \Rightarrow EB \bot BC\)
