HĐ 3
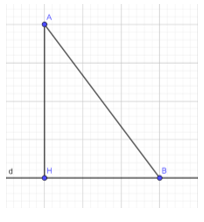
Quan sát tam giác AHB ở Hình 6.
a) Hãy cho biết trong hai góc AHB và ABH, góc nào lớn hơn
b) Từ câu a, hãy giải thích vì sao AB > AH.

- Ta sử dụng định lí về tổng số đo 3 góc trong 1 tam giác.
- Ta sử dụng định lí: Trong tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn.

a) Xét tam giác AHB vuông tại H ( theo giả thiết )
\( \Rightarrow \widehat {ABH} + \widehat {HAB} = {90^o}\)
\( \Rightarrow \widehat {AHB} > \widehat {ABH}\)( Do \(\widehat {AHB} = {90^o}\) và \(\widehat {ABH} < {90^o}\))
b) Xét tam giác AHB có:
\(\widehat {AHB} > \widehat {ABH}\)( chứng minh a )
Mà \(\widehat {AHB}\) đối diện với cạnh AB, \(\widehat {ABH}\) đối diện với cạnh AH.
\( \Rightarrow AB > AH\)
Thực hành 2
Advertisements (Quảng cáo)
Trong Hình 8, tìm đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BF. Trong số các đường này, đường nào ngắn nhất ?


Sử dụng tính chất trong các đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên

Theo hình 8 ta thấy AD là đường ngắn nhất vì AD vuông góc với BF
Các đường xiên là AB, AC, AE, AF.
Vận dụng 2
Bạn Minh xuất phát từ điểm M bên hồ bơi (Hình 9). Bạn ấy muốn tìm đường ngắn nhất để bơi đến thành hồ đối diện. Theo em, bạn Minh phải bơi theo đường nào ?


Sử dụng tính chất trong các đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên.

Ta gọi thành hồ bơi đối diện là đường thẳng AD
Bạn Minh bơi đường ngắn nhất khi bơi từ điểm M 1 đường vuông góc với AD do đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên .
Ta thấy AM vuông góc AD nên AM là đường ngắn nhất
