Giải bài 4.38 trang 87 SGK Toán lớp 7 tập 1 Kết nối tri thức với cuộc sống - Bài tập cuối chương 4 tam giác bằng nhau
![]()
Cho tam giác ABC cân tại A có ∠. Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:
a)
b) Các tam giác ANB, AMC lần lượt cân tại N, M.
![]()
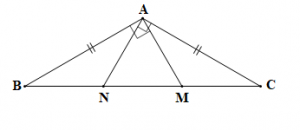
a) Tam giác ABC cân tại A (theo giả thiết) nên AB = AC và góc
tại A (theo giả thiết) nên ∠; tại A (theo giả thiết) nên ∠
Xét tam giác BAM (vuông tại A) và tam giác CAN (vuông tại A) có:
AB = AC (chứng minh trên);
(chứng minh trên).
Vậy (cạnh góc vuông – góc nhọn kề).
b) Trong tam giác ABC có ∠(định lí tổng ba góc trong một tam giác).
Suy ra ∠
Advertisements (Quảng cáo)
Mà ∠ (theo giả thiết) và ∠ (chứng minh trên).
Do đó ∠
Khi đó ∠ (1)
Ta có: ∠ (do 90° < 120°) nên tia AM nằm giữa hai tia AB và AC.
Do đó ∠
Suy ra ∠
Vậy ∠ (2)
Tương tự ta cũng có ∠.
Suy ra ∠
Vậy ∠ (3)
Từ (1), (2) và (3) ta có: ∠
Do đó tam giác ABN cân tại N (do ∠);
Và tam giác ACM cân tại M (do ∠).
