Giả sử có hai đường thẳng phân biệt đi qua A và vuông góc với d. Hướng dẫn giải Bài 1 (3.32) trang 52 vở thực hành Toán 7 - Bài tập cuối chương 3. (3. 32) Chứng minh rằng: Cho điểm A và đường thẳng d thì có duy nhất đường thẳng đi qua A...

Bài 1 (3.32) Chứng minh rằng: Cho điểm A và đường thẳng d thì có duy nhất đường thẳng đi qua A vuông góc với d, tức là nếu có hai đường thẳng đi qua A vuông góc với d thì chúng phải trùng nhau.

Giả sử có hai đường thẳng phân biệt đi qua A và vuông góc với d.
Advertisements (Quảng cáo)

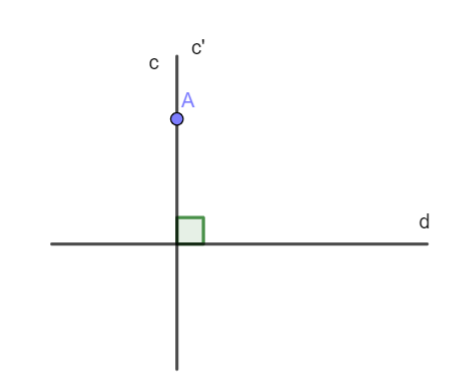
Nếu có hai đường thẳng phân biệt c, c’ cùng vuông góc với d thì c và c’ phải song aong với nhau (bài 3.25) nên c và c’ không thể có điểm chung A.
Vì vậy qua điểm A và đường thẳng d chỉ có duy nhất một đường thẳng đi qua A và vuông góc với d.
