
Cho tam giác ABC vuông tại A. Tia phân giác của góc BAC cắt BC tại D. Cho biết \(DB = 15cm,DC = 20cm\). Tính độ dài AB, AC.

Sử dụng kiến thức về tính chất của đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề đoạn ấy.

Advertisements (Quảng cáo)
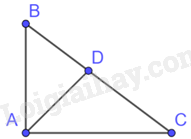
Ta có: \(BC = DC + DB = 35\left( {cm} \right)\)
Vì AD là tia phân giác của góc BAC trong tam giác ABC nên theo tính chất của đường phân giác của tam giác ta có: \(\frac{{AB}}{{AC}} = \frac{{BD}}{{DC}} = \frac{{15}}{{20}} = \frac{3}{4}\), suy ra: \(AB = \frac{3}{4}AC\)
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có: \(B{C^2} = A{B^2} + A{C^2}\), \({35^2} = \frac{9}{{16}}A{C^2} + A{C^2}\),
\(A{C^2} = 784\) nên \(AC = 28cm\), do đó \(AB = \frac{3}{4}.28 = 21\left( {cm} \right)\)
