
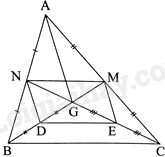
Cho tam giác ABC, hai đường trung tuyến BM và CN cắt nhau tại G \(\left( {M \in AC,N \in AB} \right)\). Gọi D, E lần lượt là trung điểm của GB, GC. Chứng minh:
a) MN//DE
b) ND//ME

+ Sử dụng kiến thức về đường trung bình của tam giác để chứng minh: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
+ Sử dụng kiến thức về tính chất của đường trung bình của tam giác để chứng minh: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Advertisements (Quảng cáo)
a) Vì BM và CN là các đường trung tuyến của tam giác ABC nên \(AM = MC,AN = NB\)
Tam giác ABC có: \(AM = MC,AN = NB\) nên MN là đường trung bình của tam giác ABC.
Do đó, \(MN//BC,MN = \frac{1}{2}BC\)
Tam giác GBC có: D, E lần lượt là trung điểm của GB, GC nên DE là đường trung bình của tam giác GBC.
Do đó, DE//BC, \(DE = \frac{1}{2}BC\)
Ta có: MN//BC, DE//BC nên MN//DE
b) Tứ giác MNDE có: MN//DE, \(MN = DE\left( { = \frac{{BC}}{2}} \right)\)
Do đó, tứ giác MNDE là hình bình hành. Do đó, ND//ME
