Cho hàm số \(y = \left( {3m + 1} \right)x - 2m\).
a) Tìm điều kiện của m để hàm số đã cho là hàm số bậc nhất.
b) Tìm m để đồ thị hàm số đã cho là đường thẳng song song với đường thẳng \(y = - 2x + 5\).
c) Với m tìm được ở câu b), hãy vẽ đồ thị của hàm số đã cho.

a) Sử dụng khái niệm hàm số bậc nhất để tìm m: Hàm số bậc nhất là hàm số cho bởi công thức \(y = ax + b,\) trong đó a, b là các số cho trước và \(a \ne 0\)
b) Sử dụng kiến thức về vị trí tương đối của hai đường thẳng để tìm m:
Cho hai đường thẳng \(\left( d \right):y = ax + b\left( {a \ne 0} \right)\,\) và \(\left( {d’} \right):y = a’x + b’\left( {a’ \ne 0} \right)\,\). Khi đó, d song song với d’ nếu \(a = a’,b \ne b’\)
c) Sử dụng kiến thức về cách vẽ đồ thị hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\) để vẽ đồ thị:
+ Khi \(b = 0\) thì \(y = ax\). Đồ thị của hàm số \(y = ax\) là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a).
+ Khi \(b \ne 0\), ta thường xác định hai điểm đặc biệt trên đồ thị là giao điểm của đồ thị với hai trục tọa độ như sau:
Advertisements (Quảng cáo)
- Cho \(x = 0\) thì \(y = b\), ta được điểm P(0; b) thuộc trục tung Oy.
- Cho \(y = 0\) thì \(x = \frac{{ - b}}{a}\), ta được điểm \(Q\left( { - \frac{b}{a};0} \right)\) thuộc trục hoành Ox.
- Vẽ đường thẳng đi qua hai điểm P, Q ta được đồ thị của hàm số \(y = ax + b\)

a) Hàm số \(y = \left( {3m + 1} \right)x - 2m\) là hàm số bậc nhất khi \(3m + 1 \ne 0\), suy ra \(m \ne \frac{{ - 1}}{3}\).
b) Vì đồ thị hàm số đã cho là đường thẳng song song với đường thẳng \(y = - 2x + 5\) nên \(3m + 1 = - 2\) và \( - 2m \ne 5\)
Suy ra, \(m = - 1\left( {tm} \right)\) và \(m \ne \frac{{ - 5}}{2}\)
Vậy \(m = - 1\)
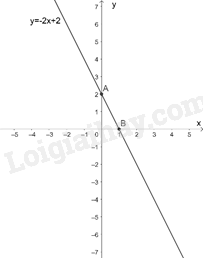
c) Với \(m = - 1\) ta có: \(y = - 2x + 2\)
Đồ thị hàm số \(y = - 2x + 2\) là đường thẳng đi qua hai điểm \(A\left( {0;2} \right),B\left( {1;0} \right)\)
Đồ thị hàm số: