Dựa vào hệ quả của định lý Thales để tính khoảng cách AB. Gợi ý giải bài 1 trang 60 SGK Toán 8 – Cánh diều Bài 2. Ứng dụng của định lí Thalès trong tam giác. Để đo khoảng cách giữa hai vị trí A và B trong đó B không tới được...Để đo khoảng cách giữa hai vị trí A và B trong đó B không tới được
Để đo khoảng cách giữa hai vị trí A và B trong đó B không tới được, người ta tiến hành chọn các vị trí C, D, E như ở Hình 24 và đo được \(AC = 50m,\,\,CD = 20m,\,\,DE = 18m\). Hỏi khoảng cách giữa hai vị trí A và B là bao nhiêu?
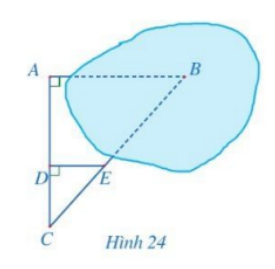
Dựa vào hệ quả của định lý Thales để tính khoảng cách AB.
Ta có:
\(\left. \begin{array}{l}AB \bot AC\\DE \bot AC\end{array} \right\} \Rightarrow AB\parallel DE\)
Xét tam giác ABC với \(AB\parallel DE\) có:
\(\frac{{DE}}{{AB}} = \frac{{CD}}{{CA}}\) (Hệ quả của định lý Thales)
\(\begin{array}{l} \Rightarrow \frac{{18}}{{AB}} = \frac{{20}}{{50}}\\ \Rightarrow AB = 18.50:20\\ \Rightarrow AB = 45\end{array}\)
Vậy khoảng cách AB là 45m.