
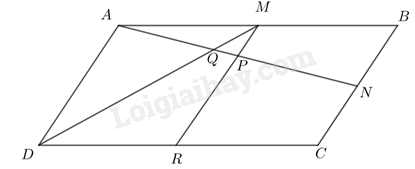
Cho hình bình hành ABCD. Gọi M, N, P lần lượt là trung điểm của các đoạn thẳng AB, BC, AN và Q là giao điểm của AN và DM. Chứng minh:
a) \(MP\parallel AD,\,\,MP = \frac{1}{4}AD\)
b) \(AQ = \frac{2}{5}AN\)
c) Gọi R là trung điểm của CD. Chứng minh ba điểm M, P, R thẳng hàng và \(PR = \frac{3}{4}AD\).

a) Chứng minh MP là đường trung bình của tam giác ABN.
b) Từ \(MP\parallel AD\), sử dụng định lý Thales để chứng minh đẳng thức.
c) Chứng minh \(MR\parallel AD\) và sử dụng các tỉ lệ đã có để chứng minh yêu cầu đề bài.


Vì M và P lần lượt là trung điểm của AB và AN nên MP là đường trung bình của tam giác ABN.
\( \Rightarrow MP\parallel BN\) hay \(MP\parallel BC\).
Advertisements (Quảng cáo)
Mà ABCD là hình bình hành nên \(AD\parallel BC\)
\( \Rightarrow MP\parallel AD\)
Ta có: \(MP = \frac{1}{2}NB\)
Mà N là trung điểm BC nên \(NB = \frac{1}{2}BC\)
\( \Rightarrow MP = \frac{1}{4}BC \Rightarrow MP = \frac{1}{4}AD\)
b) Vì \(MP\parallel AD\) nên \(\frac{{MP}}{{AD}} = \frac{{QP}}{{AQ}}\) (hệ quả của định lý Thales)
\( \Rightarrow \frac{{QP}}{{AQ}} = \frac{1}{4} \Rightarrow AQ = 4QP\,\,\left( 1 \right)\)
Ta có: \(QP = AP - AQ = \frac{1}{2}AN - AQ\) (P là trung điểm AN)
Thay vào (1) ta được \(AQ = 4.\left( {\frac{1}{2}AN - AQ} \right)\)
\( \Rightarrow AQ = 2AN - 4AQ \Rightarrow 5AQ = 2AN \Rightarrow AQ = \frac{2}{5}AN\) (đpcm)
c) Vì M và R lần lượt là trung điểm của AB và CD nên \(MR\parallel AD,\,\,MR = AD\)
Mà ta đã chứng minh \(MP\parallel AD\) nên ba điểm M, P, R thẳng hàng.
Theo câu a) ta có \(MP = \frac{1}{4}AD \Rightarrow MP = \frac{1}{4}MR\)
\( \Rightarrow PR = \frac{3}{4}MR \Rightarrow PR = \frac{3}{4}AD\).
