Hoạt động1
Quan sát hình 68 và so sánh:
a) Các tỉ số \(\frac{{A’B’}}{{AB}}\) và \(\frac{{A’C’}}{{AC}}\)
b) Các góc \(\widehat A\) và \(\widehat {A’}\)
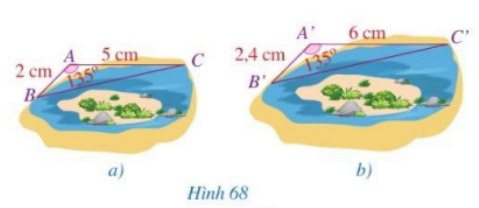

Quan sát hình và so sánh các góc và tỉ số các cạnh.

a) Ta có:
\(\begin{array}{l}\frac{{A’B’}}{{AB}} = \frac{2,4}{{2}} = \frac{6}{5}\\\frac{{A’C’}}{{AC}} = \frac{6}{5}\end{array}\)
Vậy \(\frac{{A’B’}}{{AB}} = \frac{{A’C’}}{{AC}}\)
b) Ta có: \(\widehat A = \widehat {A’} = 135^\circ \)
Luyện tập1
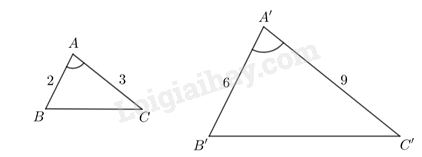
Cho hai tam giác ABC và A’B’C’ thỏa mãn \(AB = 2,AC = 3,A’B’ = 6,A’C’ = 9\) và \(\widehat A = \widehat {A’}\). Chứng minh \(\widehat B = \widehat {B’},\,\,\widehat C = \widehat {C’}\).

Chứng minh hai tam giác đồng dạng theo trường hợp đồng dạng thứ hai rồi suy ra các góc bằng nhau theo định nghĩa tam giác đồng dạng.

Advertisements (Quảng cáo)
Ta thấy
\(\begin{array}{l}\frac{{AB}}{{A’B’}} = \frac{2}{6} = \frac{1}{3}\\\frac{{AC}}{{A’C’}} = \frac{3}{9} = \frac{1}{3}\\ \Rightarrow \frac{{AB}}{{A’B’}} = \frac{{AC}}{{A’C’}}\end{array}\)
Xét tam giác ABC và tam giác A’B’C’ có:
\(\frac{{AB}}{{A’B’}} = \frac{{AC}}{{A’C’}}\) và \(\widehat A = \widehat {A’}\)
\( \Rightarrow \Delta ABC \backsim \Delta A’B’C’\) (c-g-c)
\( \Rightarrow \)\(\widehat B = \widehat {B’},\,\,\widehat C = \widehat {C’}\)
Luyện tập2
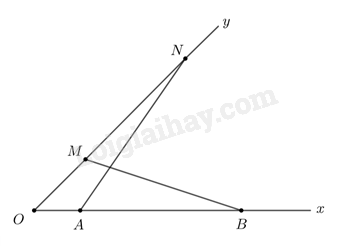
Cho góc \(xOy\). Trên tia Ox lấy các điểm A, B sao cho \(OA = 2cm,\,\,OB = 9cm\). Trên tia Oy lấy các điểm M, N sao cho \(OM = 3cm,\,\,ON = 6cm\). ChỨNG minh \(\widehat {OBM} = \widehat {ONA}\).

Chứng minh hai tam giác OAN và OMB đồng dạng theo trường hợp đồng dạng thứ hai rồi suy ra các góc bằng nhau theo định nghía tam giác đồng dạng.

Ta thấy
\(\begin{array}{l}\frac{{OA}}{{OM}} = \frac{2}{3};\,\,\frac{{ON}}{{OB}} = \frac{6}{9} = \frac{2}{3}\\ \Rightarrow \frac{{OA}}{{OM}} = \frac{{ON}}{{OB}}\end{array}\)
Xét tam giác OAN và tam giác OMB có:
\(\frac{{OA}}{{OM}} = \frac{{ON}}{{OB}}\) và \(\widehat O\) chung
\( \Rightarrow \Delta OAN \backsim \Delta OMB\) (c-g-c)
\( \Rightarrow \widehat {OBM} = \widehat {ONA}\)
