Hoạt động2
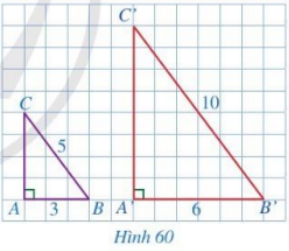
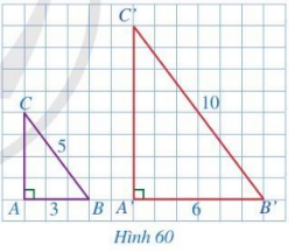
Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ (Hình 60) sao cho \(AB = 3,\,\,BC = 5,\,\,A’B’ = 6,\,\,B’C’ = 10\).
a) Tính CA và C’A’
b) So sánh các tỉ số \(\frac{{A’B’}}{{AB}};\,\,\frac{{A’C’}}{{AC}};\,\,\frac{{B’C’}}{{BC}}\)
c) Hai tam giác A’B’C’ và ABC có đồng dạng với nhau hay không?

a) Dựa vào định lý Pytago để tính độ dài CA và C’A’.
b) Tính các tỉ số rồi so sánh.
c) Dựa vào trường hợp đồng dạng thứ nhất của tam giác để xét đồng dạng.

a) Xét tam giác ABC vuông tại A ta có:
\(A{B^2} + A{C^2} = B{C^2}\) (Định lý Pytago)
\(\begin{array}{l} \Rightarrow {3^2} + C{A^2} = {5^2}\\ \Leftrightarrow C{A^2} = {5^2} - {3^2}\\ \Leftrightarrow C{A^2} = 16\\ \Leftrightarrow CA = 4\end{array}\)
Xét tam giác A’B’C’ vuông tại A’ ta có:
\(A’B{‘^2} + A’C{‘^2} = B’C{‘^2}\) (Định lý Pytago)
\(\begin{array}{l} \Rightarrow {6^2} + A’C{‘^2} = {10^2}\\ \Leftrightarrow A’C{‘^2} = {10^2} - {6^2}\\ \Leftrightarrow A’C{‘^2} = 64\\ \Leftrightarrow A’C’ = 8\end{array}\)
b) Ta có:
\(\begin{array}{l}\frac{{A’B’}}{{AB}} = \frac{6}{3} = 2\\\frac{{B’C’}}{{BC}} = \frac{{10}}{5} = 2\\\frac{{C’A’}}{{CA}} = \frac{8}{4} = 2\end{array}\)
Ta thấy \(\frac{{A’B’}}{{AB}} = \frac{{A’C’}}{{AC}} = \frac{{B’C’}}{{BC}}\).
Advertisements (Quảng cáo)
c) Xét tam giác A’B’C’ và tam giác ABC có: \(\frac{{A’B’}}{{AB}} = \frac{{A’C’}}{{AC}} = \frac{{B’C’}}{{BC}}\)
\( \Rightarrow \Delta A’B’C’ \backsim\Delta ABC\) (c-c-c)
Luyện tập2
Trong Hình 64, chứng minh tam giác \(CDM\)vuông tại \(M\).
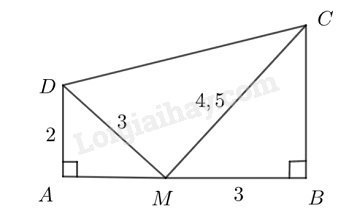
Hình 64

- Chứng minh \(\Delta ADM \backsim\Delta BMC\)
- Suy ra \(\widehat {AMD} = \widehat {BCM}\) và \(\widehat {ADM} = \widehat {BMC}\)
- Dựa vào tính chất tổng hai góc nhọn trong tam giác vuông bằng \(90^\circ \) ta chứng minh \(\widehat {AMD} + \widehat {BMC} = 90^\circ \)
- Suy ra \(\widehat {DMC} = 90^\circ \) hay tam giác \(CDM\)vuông tại \(M\).

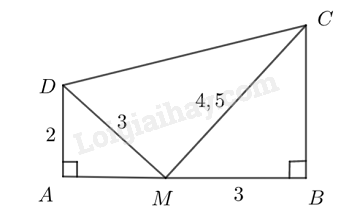
Vì \(\frac{{AD}}{{BM}} = \frac{2}{3},\,\,\frac{{DM}}{{MC}} = \frac{3}{{4,5}} = \frac{2}{3}\) nên \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\).
Xét hai tam giác \(ADM\) và \(BMC\) có \(\widehat {MAD} = \widehat {CBM} = 90^\circ \) và \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\) nên \(\Delta{ADM} \backsim \Delta{BMC}\).
Suy ra \(\widehat {AMD} = \widehat {BCM}\) và \(\widehat {ADM} = \widehat {BMC}\).
Xét tam giác \(ADM\) vuông tại A có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\widehat {AMD} + \widehat {ADM} = 90^\circ \\ \Rightarrow \widehat {AMD} + \widehat {BMC} = 90^\circ \end{array}\)
Mà ta có:
\(\begin{array}{l}\,\,\,\,\,\widehat {AMD} + \widehat {DMC} + \widehat {CMB} = 180^\circ \\ \Rightarrow 90^\circ + \widehat {DMC} = 180^\circ \\ \Rightarrow \widehat {DMC} = 90^\circ \end{array}\)
Vậy tam giác \(CDM\)vuông tại \(M\).
