Vẽ một hệ trục tọa độ \(Oxy\) và đánh dấu các điểm \(A\left( { - 2;0} \right);B\left( {0;4} \right);C\left( {5;4} \right);D\left( {3;0} \right)\). Tứ giác \(ABCD\) là hình gì?
- Điểm \(M\left( {{x_0};{y_0}} \right)\) nghĩa là hoành độ của điểm \(M\) là \({x_0}\) và tung độ của điểm \(M\) là \({y_0}\).
- Hai điểm có cùng tung độ thì đoạn thẳng nối hai điểm đó song song với trục hoành.
- Hai điểm có cùng tung độ thì độ dài đoạn thẳng nối hai điểm đó bằng giá trị tuyệt đối của hiệu hai hoành độ.
\(A\left( { - 2;0} \right)\) \( \Rightarrow \) hoành độ của điểm \(A\) là –2 và tung độ của điểm \(A\) là 0.
\(B\left( {0;4} \right)\) \( \Rightarrow \) hoành độ của điểm \(B\) là 0 và tung độ của điểm \(B\) là 4.
\(C\left( {5;4} \right)\) \( \Rightarrow \) hoành độ của điểm \(C\) là 5 và tung độ của điểm \(C\) là 4.
\(D\left( {3;0} \right)\) \( \Rightarrow \) hoành độ của điểm \(D\) là 3 và tung độ của điểm \(D\) là 0.
Biểu diễn các điểm \(A;B;C;D\) trên mặt phẳng tọa độ ta được:
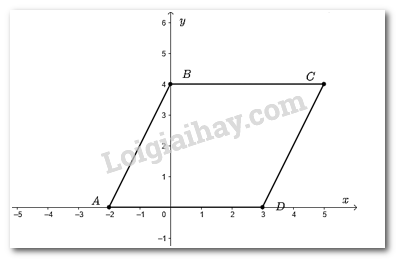
Vì hai điểm \(B;C\) có tung độ bằng nhau nên \(BC\) song song với \(Ox\); Hai điểm \(A;D\) có tung độ bằng nhau nên \(AD\) song song với \(Ox\).
Do đó, \(BC//AD\).
Lại có, \(AD = \left| {3 - \left( { - 2} \right)} \right| = 5;BC = \left| {5 - 0} \right| = 5\). Do đó, \(AD = BC\).
Xét tứ giác \(ABCD\)có:
\(AD = BC\)
\(BC//AD\)
Do đó, tứ giác \(ABCD\) là hình bình hành.